广东省中山市2018-2019学年高二下学期文数期末考试试卷

试卷更新日期：2020-06-28 类型：期末考试

进入出卷网下载

一、单选题

1. $i$ 是虚数单位，则 $\frac{1 - 2 i}{i}$ 的虚部是（）

A、-2 B、-1 C、 $- i$ D、 $- 2 i$

查看试题解析
2. 用反证法证明“方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 至多有两个解”的假设中，正确的是（）

A、至少有两个解 B、有且只有两个解 C、至少有三个解 D、至多有一个解

查看试题解析
3. 若抛物线 $x^{2} = a y$ 的焦点到准线的距离为1，则 $a =$ （）

A、2 B、4 C、 $\pm 2$ D、 $\pm 4$

查看试题解析
4. “ $2^{a} > 2^{b}$ ”是“ $a^{3} > b^{3}$ ”（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r与残差平方和m如表：
甲
乙
丙
丁
R
0.82
0.78
0.69
0.85
M
106
115
124
103
则哪位同学的试验结果体现A、B两变量有更强的线性相关性（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 二分法是求方程近似解的一种方法，其原理是“一分为二，无限逼近”．执行如图所示的程序框图，若输入 $x_{1} = 1$ ， $x_{2} = 2$ ， $d = 0.1$ ，则输出n的值为（）

A、2 B、3 C、4 D、5

查看试题解析

7. 通过随机询问110名不同的大学生是否爱好某项运动，得到如下的列联表：

	男	女	总计
爱好	40	20	60
不爱好	20	30	50
总计	60	50	110

由 $K^{^{2}} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} 算得， K^{^{2}} = \frac{110 \times {(40 \times 30 - 20 \times 30)}^{2}}{60 \times 50 \times 60 \times 50} \approx 7.8$

附表：

P（K²≥k）	0.050	0.010	0.001
$k$	3.841	6.635	10.828

参照附表，得到的正确结论是（）

A、有99%以上的把握认为“爱好该项运动与性别有关” B、有99%以上的把握认为“爱好该项运动与性别无关” C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关” D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

查看试题解析

8. ${(a + b)}^{n} (n \in N^{*})$ ，当n＝1，2，3，4，5，6时展开式的二项式系数表示形式

借助上面的表示形式，判断λ与μ的值分别是（）

A、5，9 B、5，10 C、6，10 D、6，9

查看试题解析
9. 已知函数 $f (x) = \frac{\ln x}{x}$ ，若 $a = f (2)$ ， $b = f (3)$ ， $c = f (5)$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $b < c < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $c < a < b$

查看试题解析
10. 已知 $F_{1}$ ， $F_{2}$ 为椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左，右焦点， $B$ 为 $C$ 的短轴的一个端点，直线 $B F_{1}$ 与 $C$ 的另一个交点为 $A$ ，若 $Δ B A F_{2}$ 为等腰三角形，则 $\frac{| A F_{1} |}{| A F_{2} |} =$ （）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析
11. 函数 $f (x) = x^{2} + x sin x$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
12. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a ， b > 0)$ ，过 $x$ 轴上点 $P$ 的直线 $l$ 与双曲线的右支交于 $M ， N$ 两点（ $M$ 在第一象限），直线 $M O$ 交双曲线左支于点 $Q$ （ $O$ 为坐标原点），连接 $Q N$ ，若 $∠ M P O = 60 °$ ， $∠ M N Q = 30 °$ ，则该双曲线的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、4

查看试题解析

二、填空题

13. 曲线 $y ＝ x e^{x} + 2 x ﹣ 1$ 在点 $(0 ， - 1)$ 处的切线方程为．

查看试题解析
14. 若命题“ $\exists x_{0} \in R ， 3 x_{0}^{2} + 2 a x_{0} + 1 < 0$ ”是假命题，则实数a的取值范围是.

查看试题解析
15. 要设计一个容积为 $π$ 的下端为圆柱形、上端为半球形的密闭储油罐，已知圆柱侧面的单位面积造价是下底面积的单位面积造价的一半，而顶部半球面的单位面积造价又是圆柱侧面的单位面积造价的一半，储油罐的下部圆柱的底面半径 $R =$ 时，造价最低．

查看试题解析
16. 有甲、乙二人去看望高中数学张老师，期间他们做了一个游戏，张老师的生日是 $m$ 月 $n$ 日，张老师把 $m$ 告诉了甲，把 $n$ 告诉了乙，然后张老师列出来如下10个日期供选择： 2月5日，2月7日，2月9日，3月2日，3月7日，5月5日，5月8日，7月2日，7月6日，7月9日．看完日期后，甲说“我不知道，但你一定也不知道”，乙听了甲的话后，说“本来我不知道，但现在我知道了”，甲接着说，“哦，现在我也知道了”．请问张老师的生日是．

查看试题解析

三、解答题

17. 求证： $\sqrt{7} - \sqrt{5} > 2 \sqrt{2} - \sqrt{6}$

查看试题解析
18. 已知复数 $z = {(a + i)}^{2} ， w = 4 - 3 i$ 其中 $a$ 是实数，

(1)、若在复平面内表示复数 $z$ 的点位于第一象限，求 $a$ 的范围；

(2)、若 $\frac{z}{w}$ 是纯虚数， $a$ 是正实数，
①求 $a$ ，

②求 $\frac{z}{w} + {(\frac{z}{w})}^{2} + {(\frac{z}{w})}^{3} + ... + {(\frac{z}{w})}^{2019}$ ；

查看试题解析

19. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近

6

个月广告投入量

x

（单位：万元）和收益

y

（单位：万元）的数据如下表：

月份	$1$	$2$	$3$	$4$	$5$	$6$
广告投入量	$2$	$4$	$6$	$8$	$10$	$12$
收益	$14.21$	$20.31$	$31.8$	$31.18$	$37.83$	$44.67$

他们分别用两种模型① $y = b x + a$ ，② $y = a e^{b x}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

$\bar{x}$	$\bar{y}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\sum_{i = 1}^{6} x_{i}^{2}$
$7$	$30$	$1464.24$	$364$

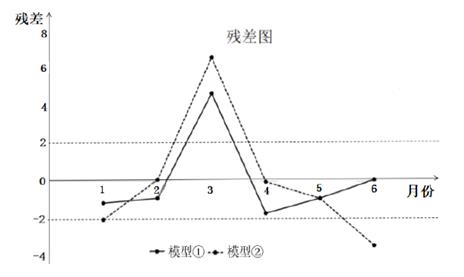
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $2$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $x = 18$ 时，该模型收益的预报值是多少？

附：对于一组数据 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，……， $(x_{n} ， y_{n})$ ，其回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘估计分别为：

 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ $= \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ .

查看试题解析

20. 已知圆 $O ： x^{2} + y^{2} ＝ r^{2}$ ，椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的短半轴长等于圆 $O$ 的半径，且过 $C$ 右焦点的直线与圆 $O$ 相切于点 $D (\frac{1}{2} ， \frac{\sqrt{3}}{2})$ ．

(1)、求椭圆 $C$ 的方程；

(2)、若动直线 $l$ 与圆 $O$ 相切，且与 $C$ 相交于 $A ， B$ 两点，求点 $O$ 到弦 $A B$ 的垂直平分线距离的最大值．

查看试题解析
21. 设函数 $f (x) = e^{x} + \frac{x^{2}}{m^{2}} - x$ ．

(1)、求 $f (x)$ 的单调区间；

(2)、若对于任意 $x_{1} ， x_{2} \in [- m ， m] (m > 0)$ ，都有 $| f (x_{1}) - f (x_{2}) | \leq e - 1$ ，求 $m$ 的取值范围．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{matrix} x = 2 + t ， \\ y = 1 + \sqrt{3} t \end{matrix}$ （ $t$ 为参数），曲线 $C$ 的参数方程为 ${\begin{matrix} x = 4 + 2 c o s θ \\ y = 3 + 2 s i n θ \end{matrix}$ （ $θ$ 为参数），以坐标原点为极点， $x$ 轴非负半轴为极轴建立极坐标系.

(1)、求 $C$ 的极坐标方程；

(2)、设点 $M (2 ， 1)$ ，直线 $l$ 与曲线 $C$ 相交于点 $A ， B$ ，求 $| M A | \cdot | M B |$ 的值.

查看试题解析
23. 已知 $P （ 1 ， 0 ）$ .

(1)、求 $f (x) \leq 1$ 的解集；

(2)、若 $f (x^{2}) \geq a | x |$ 恒成立，求实数 $a$ 的最大值.

查看试题解析

	甲	乙	丙	丁
R	0.82	0.78	0.69	0.85
M	106	115	124	103