广东省中山市2018-2019学年高二下学期理数期末考试试卷

试卷更新日期：2020-06-28 类型：期末考试

进入出卷网下载

一、单选题

1. $i$ 是虚数单位，则 $\frac{1 - 2 i}{i}$ 的虚部是（）

A、-2 B、-1 C、 $- i$ D、 $- 2 i$

查看试题解析
2. 用反证法证明“方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 至多有两个解”的假设中，正确的是（）

A、至少有两个解 B、有且只有两个解 C、至少有三个解 D、至多有一个解

查看试题解析
3. 已知函数 $f (x)$ 的导函数为 $f' (x)$ ，且满足 $f (x) = x^{2} + f' (2) \ln x$ ，则 $f' (2)$ 的值为（）

A、6 B、7 C、8 D、9

查看试题解析
4. 甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r与残差平方和m如表：
甲
乙
丙
丁
R
0.82
0.78
0.69
0.85
M
106
115
124
103
则哪位同学的试验结果体现A、B两变量有更强的线性相关性（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
5. 在数学归纳法的递推性证明中，由假设 $n = k$ 时成立推导 $n = k + 1$ 时成立时， $f (n) =$ $1$ $+$ $\frac{1}{2} + \frac{1}{3} + \cdot \cdot \cdot + \frac{1}{2^{n} - 1}$ 增加的项数是（）

A、 $1$ B、 $2^{k} + 1$ C、 $2^{k}$ D、 $2^{k} - 1$

查看试题解析
6. 已知 $Z ~ N (10 ， 4)$ ，则 $P (Z < 6) \approx$ （）
附：若 $X \sim N (μ ， σ^{2})$ ，则 $P (μ - σ < X < μ + σ) \approx 0.6826$ ， $P (μ - 2 σ < X < μ + 2 σ) \approx 0.9544$

A、0.3174 B、0.1587 C、0.0456 D、0.0228

查看试题解析
7. 已知 $X$ 是离散型随机变量， $P (X = 1) = \frac{1}{4}$ ， $P (X = a) = \frac{3}{4}$ ， $E (X) = \frac{7}{4}$ ，则 $D (2 X - 1) =$ （）

A、 $\frac{2}{5}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{5}{6}$

查看试题解析
8. $C_{3}^{0} + C_{4}^{1} + C_{5}^{2} + \dots + C_{21}^{18}$ 的值等于（）

A、7351 B、7355 C、7513 D、7315

查看试题解析
9. 已知函数 $f (x) = \frac{\ln x}{x}$ ，若 $a = f (2)$ ， $b = f (3)$ ， $c = f (5)$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $b < c < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $c < a < b$

查看试题解析
10. 函数 $f (x) = x^{2} + x sin x$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
11. 某次考试共有12个选择题，每个选择题的分值为5分，每个选择题四个选项且只有一个选项是正确的， $A$ 学生对12个选择题中每个题的四个选择项都没有把握，最后选择题的得分为 $X$ 分， $B$ 学生对12个选择题中每个题的四个选项都能判断其中有一个选项是错误的，对其它三个选项都没有把握，选择题的得分为 $Y$ 分，则 $D (Y) - D (X)$ 的值为（）

A、 $\frac{125}{12}$ B、 $\frac{35}{12}$ C、 $\frac{27}{4}$ D、 $\frac{23}{4}$

查看试题解析
12. 杨辉三角，是二项式系数在三角形中的一种几何排列.在欧洲，这个表叫做帕斯卡三角形，帕斯卡（1623-1662）是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，这是我国数学史上的一个伟大成就.如图所示，在“杨辉三角”中，去除所有为1的项，依次构成数列 $2 ， 3 ， 3 ， 4 ， 6 ， 4 ， 5 ， 10 ， 10 ， 5 \dots$ ，则此数列前135项的和为（）

A、 $2^{18} - 53$ B、 $2^{18} - 52$ C、 $2^{17} - 53$ D、 $2^{17} - 52$

查看试题解析

二、填空题

13. 曲线 $y ＝ x e^{x} + 2 x ﹣ 1$ 在点 $(0 ， - 1)$ 处的切线方程为．

查看试题解析
14. 某地环保部门召集6家企业的负责人座谈，其中甲企业有2人到会，其余5家企业各有1人到会，会上有3人发言，则发言的3人来自3家不同企业的可能情况的总数为．

查看试题解析
15. 要设计一个容积为 $π$ 的下端为圆柱形、上端为半球形的密闭储油罐，已知圆柱侧面的单位面积造价是下底面积的单位面积造价的一半，而顶部半球面的单位面积造价又是圆柱侧面的单位面积造价的一半，储油罐的下部圆柱的底面半径 $R =$ 时，造价最低．

查看试题解析
16. 有甲、乙二人去看望高中数学张老师，期间他们做了一个游戏，张老师的生日是 $m$ 月 $n$ 日，张老师把 $m$ 告诉了甲，把 $n$ 告诉了乙，然后张老师列出来如下10个日期供选择： 2月5日，2月7日，2月9日，3月2日，3月7日，5月5日，5月8日，7月2日，7月6日，7月9日．看完日期后，甲说“我不知道，但你一定也不知道”，乙听了甲的话后，说“本来我不知道，但现在我知道了”，甲接着说，“哦，现在我也知道了”．请问张老师的生日是．

查看试题解析

三、解答题

17. 若 ${(x \sqrt{x} + \frac{1}{x^{4}})}^{n}$ 的展开式中，第二、三、四项的二项式系数成等差数列．

(1)、求 $n$ 的值；

(2)、此展开式中是否有常数项，为什么？

查看试题解析
18. 请先阅读：在等式 $\cos 2 x = 2 \cos^{2} x - 1 (x \in R)$ 的两边求导，得： ${(\cos 2 x)}^{'} = {(2 \cos^{2} x - 1)}^{'}$ ，由求导法则，得： $(- \sin 2 x) \cdot 2 = 4 \cos x \cdot (- \sin x)$ ，化简得等式： $\sin 2 x = 2 \cos x \cdot \sin x$ ．利用上述的想法，结合等式 ${(1 + x)}^{n} = C_{n}^{0} + C_{n}^{1} \cdot x + C_{n}^{2} \cdot x^{2} + \dots + C_{n}^{n} \cdot x^{n}$ （ $x \in R$ ，正整数 $n \geq 2$ ）

(1)、求 $C_{10}^{1} + 2 C_{10}^{2} + 3 C_{10}^{3} + \dots + 10 C_{10}^{10}$ 的值；

(2)、求 $1^{2} C_{10}^{1} + 2^{2} C_{10}^{2} + 3^{2} C_{10}^{3} + \dots + 10^{2} C_{10}^{10}$ 的值．

查看试题解析

19. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近

6

个月广告投入量

x

（单位：万元）和收益

y

（单位：万元）的数据如下表：

月份	$1$	$2$	$3$	$4$	$5$	$6$
广告投入量	$2$	$4$	$6$	$8$	$10$	$12$
收益	$14.21$	$20.31$	$31.8$	$31.18$	$37.83$	$44.67$

他们分别用两种模型① $y = b x + a$ ，② $y = a e^{b x}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如图所示的残差图及一些统计量的值：

$\bar{x}$	$\bar{y}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\sum_{i = 1}^{6} x_{i}^{2}$
$7$	$30$	$1464.24$	$364$

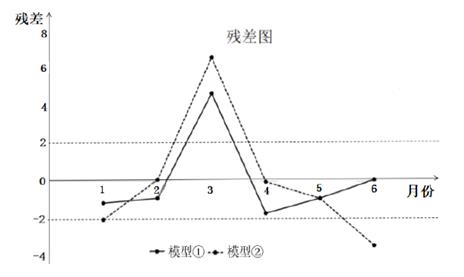
（Ⅰ）根据残差图，比较模型①，②的拟合效果，应选择哪个模型？并说明理由；

（Ⅱ）残差绝对值大于 $2$ 的数据被认为是异常数据，需要剔除：

（ⅰ）剔除异常数据后求出（Ⅰ）中所选模型的回归方程；

（ⅱ）若广告投入量 $x = 18$ 时，该模型收益的预报值是多少？

附：对于一组数据 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ，……， $(x_{n} ， y_{n})$ ，其回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘估计分别为：

 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ $= \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ .

查看试题解析

20. 某工厂共有男女员工500人，现从中抽取100位员工对他们每月完成合格产品的件数统计如下：

每月完成合格产品的件数（单位：百件）	$[26 ， 28)$	$[28 ， 30)$	$[30 ， 32)$	$[32 ， 34)$	$[34 ， 36]$
频数	10	45	35	6	4
男员工人数	7	23	18	1	1

(1)、其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面

2 \times 2

列联表，并判断是否有95%的把握认为“生产能手”与性别有关？

	非“生产能手”	“生产能手”	合计
男员工
女员工
合计

(2)、为提高员工劳动的积极性，工厂实行累进计件工资制：规定每月完成合格产品的件数在定额2600件以内的，计件单价为1元；超出

(0 ， 200]

件的部分，累进计件单价为1.2元；超出

(200 ， 400]

件的部分，累进计件单价为1.3元；超出400件以上的部分，累进计件单价为1.4元.将这4段中各段的频率视为相应的概率，在该厂男员工中选取1人，女员工中随机选取2人进行工资调查，设实得计件工资（实得计件工资=定额计件工资+超定额计件工资）不少于3100元的人数为，求的分布列和数学期望.

附： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，

查看试题解析

21. 已知函数 $f (x) = (a x - x^{2}) e^{x} (a \geq 0)$ ．

(1)、若函数 $f (x)$ 在区间 $[2 ， + \infty)$ 上单调递减，求实数 $a$ 的取值范围；

(2)、设 $f (x)$ 的两个极值点为 $x_{1} ， x_{2} (x_{2} > x_{1})$ ，证明：当 $a \geq \frac{2 \sqrt{11}}{5}$ 时， $f (x_{1}) + f (x_{2}) > 0$ ．（附注： $ln 11 \approx 2.398$ ）

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{matrix} x = 2 + t, \\ y = 1 + \sqrt{3} t \end{matrix}$ （ $t$ 为参数），曲线 $C$ 的参数方程为 ${\begin{matrix} x = 4 + 2 c o s θ \\ y = 3 + 2 s i n θ \end{matrix}$ （ $θ$ 为参数），以坐标原点为极点， $x$ 轴非负半轴为极轴建立极坐标系.

(1)、求 $C$ 的极坐标方程；

(2)、设点 $M (2, 1)$ ，直线 $l$ 与曲线 $C$ 相交于点 $A, B$ ，求 $| M A | \cdot | M B |$ 的值.

查看试题解析
23. 已知 $P （ 1 ， 0 ）$ .

(1)、求 $f (x) \leq 1$ 的解集；

(2)、若 $f (x^{2}) \geq a | x |$ 恒成立，求实数 $a$ 的最大值.

查看试题解析

	甲	乙	丙	丁
R	0.82	0.78	0.69	0.85
M	106	115	124	103