广东省深圳市宝安区2018-2019学年高二下学期理数期末考试试卷
试卷更新日期:2020-06-28 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. ( 为虚数单位),则复数 对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知顶点在 轴上的双曲线实轴长为4,其两条渐近线方程为 ,该双曲线的焦点为( )A、 B、 C、 D、4. 已知函数 ,则 ( )A、 B、 C、1 D、75. 在 中, , , ,点 满足 ,则 等于( )A、10 B、9 C、8 D、76. 如图,在平面直角坐标系 中,质点 间隔3分钟先后从点 ,绕原点按逆时针方向作角速度为 弧度/分钟的匀速圆周运动,则 与 的纵坐标之差第4次达到最大值时, 运动的时间为( )
 A、37.5分钟 B、40.5分钟 C、49.5分钟 D、52.5分钟7. 下图是一个几何体的三视图,则该几何体的体积为( )
A、37.5分钟 B、40.5分钟 C、49.5分钟 D、52.5分钟7. 下图是一个几何体的三视图,则该几何体的体积为( ) A、 B、 C、 D、8. “ ”是“圆 : 与圆 : 外切”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分条件也不必要条件9. 已知点 在抛物线 的准线上, 为 的焦点,过 点的直线与 相切于点 ,则 的面积为( )A、1 B、2 C、 D、410. 已知 为等腰三角形,满足 , ,若 为底 上的动点,则 ( )A、有最大值 B、是定值 C、有最小值 D、是定值11. 函数 的图象大致为( )A、
A、 B、 C、 D、8. “ ”是“圆 : 与圆 : 外切”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分条件也不必要条件9. 已知点 在抛物线 的准线上, 为 的焦点,过 点的直线与 相切于点 ,则 的面积为( )A、1 B、2 C、 D、410. 已知 为等腰三角形,满足 , ,若 为底 上的动点,则 ( )A、有最大值 B、是定值 C、有最小值 D、是定值11. 函数 的图象大致为( )A、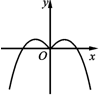 B、
B、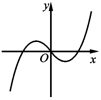 C、
C、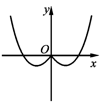 D、
D、 12. 已知双曲线 的左、右焦点分别为 、 , 、 分别是双曲线左、右两支上关于坐标原点 对称的两点,且直线 的斜率为 . 、 分别为 、 的中点,若原点 在以线段 为直径的圆上,则双曲线的离心率为( )A、 B、 C、 D、
12. 已知双曲线 的左、右焦点分别为 、 , 、 分别是双曲线左、右两支上关于坐标原点 对称的两点,且直线 的斜率为 . 、 分别为 、 的中点,若原点 在以线段 为直径的圆上,则双曲线的离心率为( )A、 B、 C、 D、二、填空题
-
13. 若x , y满足 ,则 的最小值为14. 在 的展开式中常数项等于15. 已知双曲线 的左右焦点分别为 、 ,点 在双曲线上,点 的坐标为 ,且 到直线 , 的距离相等,则16. 在 中,内角 所对的边分别为 , 是 的中点,若 且 ,则 面积的最大值是
三、解答题
-
17. 各项均为正数的数列 的首项 ,前 项和为 ,且 .(1)、求 的通项公式:(2)、若数列 满足 ,求 的前 项和 .18. 如图,在四面体 中, , 分别是线段 , 的中点, , , ,直线 与平面 所成的角等于 .
 (1)、证明:平面 平面 ;(2)、求二面角 的余弦值.19. 如图,OA,OB是两条互相垂直的笔直公路,半径OA=2km的扇形AOB是某地的一名胜古迹区域.当地政府为了缓解该古迹周围的交通压力,欲在圆弧AB上新增一个入口P(点P不与A,B重合),并新建两条都与圆弧AB相切的笔直公路MB,MN,切点分别是B,P.当新建的两条公路总长最小时,投资费用最低.设∠POA= ,公路MB,MN的总长为 .
(1)、证明:平面 平面 ;(2)、求二面角 的余弦值.19. 如图,OA,OB是两条互相垂直的笔直公路,半径OA=2km的扇形AOB是某地的一名胜古迹区域.当地政府为了缓解该古迹周围的交通压力,欲在圆弧AB上新增一个入口P(点P不与A,B重合),并新建两条都与圆弧AB相切的笔直公路MB,MN,切点分别是B,P.当新建的两条公路总长最小时,投资费用最低.设∠POA= ,公路MB,MN的总长为 . (1)、求 关于 的函数关系式,并写出函数的定义域;(2)、当 为何值时,投资费用最低?并求出 的最小值.20. 中国已经成为全球最大的电商市场,但是实体店仍然是消费者接触商品和品牌的重要渠道.某机构随机抽取了年龄介于10岁到60岁的消费者200人,对他们的主要购物方式进行问卷调查.现对调查对象的年龄分布及主要购物方式进行统计,得到如下图表:
(1)、求 关于 的函数关系式,并写出函数的定义域;(2)、当 为何值时,投资费用最低?并求出 的最小值.20. 中国已经成为全球最大的电商市场,但是实体店仍然是消费者接触商品和品牌的重要渠道.某机构随机抽取了年龄介于10岁到60岁的消费者200人,对他们的主要购物方式进行问卷调查.现对调查对象的年龄分布及主要购物方式进行统计,得到如下图表:
主要购物方式
年龄阶段
网络平台购物
实体店购物
总计
40岁以下
75
40岁或40岁以上
55
总计
(1)、根据已知条件完成上述列联表,并据此资料,能否在犯错误的概率不超过 的前提下,认为消费者主要的购物方式与年龄有关?(2)、用分层抽样的方法从通过网络平台购物的消费者中随机抽取8人,然后再从这8名消费者中抽取5名进行答谢.设抽到的消费者中40岁以下的人数为 ,求 的分布列和数学期望.参考公式: ,其中 .
临界值表:
