浙教版数学八年级上册第三章 一元一次不等式 单元测试卷
试卷更新日期:2017-09-21 类型:单元试卷
一、单选题
-
1. 数学表达式①﹣5<7;②3y﹣6>0;③a=6;④2x﹣3y;⑤a≠2;⑥7y﹣6>y+2,其中是不等式的有( )A、2个 B、3个 C、4个 D、5个2. 如果不等式组无解,那么m的取值范围是( )A、m≤3 B、m≥3 C、m>3 D、m<33. 不等式组的解集在数轴上表示正确的是( )A、
 B、
B、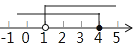 C、
C、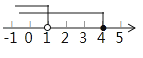 D、
D、 4. 已知a<b,下列不等式变形中正确的是( )A、a﹣2>b﹣2 B、> C、﹣2a>﹣2b D、3a+1>3b+15. 某种商品的进价为1200元,标价为1575元,后来由于该商品积压,商店准备打折出售,但要保持利润不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折6. 下列不等式组中,是一元一次不等式组的是( )A、 B、 C、 D、7. 已知关于x的不等式(1﹣a)x>2的解集为x< ,则a的取值范围是( )A、a>0 B、a>1 C、a<0 D、a<18. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.A、12 B、13 C、14 D、159. 若不等式组有实数解,则实数m的取值范围是( )A、m≤ B、m< C、m> D、m≥10. 解不等式组: 的解集是( )A、x≤﹣2 B、﹣2≤x<2 C、x<2 D、x≥﹣2
4. 已知a<b,下列不等式变形中正确的是( )A、a﹣2>b﹣2 B、> C、﹣2a>﹣2b D、3a+1>3b+15. 某种商品的进价为1200元,标价为1575元,后来由于该商品积压,商店准备打折出售,但要保持利润不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折6. 下列不等式组中,是一元一次不等式组的是( )A、 B、 C、 D、7. 已知关于x的不等式(1﹣a)x>2的解集为x< ,则a的取值范围是( )A、a>0 B、a>1 C、a<0 D、a<18. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.A、12 B、13 C、14 D、159. 若不等式组有实数解,则实数m的取值范围是( )A、m≤ B、m< C、m> D、m≥10. 解不等式组: 的解集是( )A、x≤﹣2 B、﹣2≤x<2 C、x<2 D、x≥﹣2二、填空题
-
11. 已知x<y,试比较大小:﹣2x﹣2y.12. 不等式2x+6>3x+4的正整数解是 .13.
关于x的不等式x﹣3>的解集在数轴上表示如图所示,则a的值是
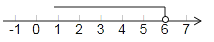 14. 不等式组 的解集为 .15. 某超市从厂家以每件21元的价格购进一批商品,该超市可以自行定价,但物价局限定每件商品加价不能超过售价的20%,则这批商品的售价不能超过元.
14. 不等式组 的解集为 .15. 某超市从厂家以每件21元的价格购进一批商品,该超市可以自行定价,但物价局限定每件商品加价不能超过售价的20%,则这批商品的售价不能超过元.三、解答题
-
16. 解下列不等式,并把它的解集在数轴上表示出来.
3x+(13﹣x)>17.
17. 求不等式组 的整数解.18. 用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:原料
甲
乙
维生素C的含量/(单位/kg)
600
100
原料价格/(元/kg)
8
4
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.
四、综合题
-
19. 已知一元一次不等式mx﹣3>2x+m.(1)、若它的解集是x< , 求m的取值范围(2)、若它的解集是x> , 试问:这样的m是否存在?如果存在,求出它的值;如果不存在,请说明理由.20. 综合题。(1)、解方程:x2﹣4x﹣3=0(2)、解不等式组: 并将解集在数轴上表示出来.21. 我们知道不等式的两边加(或减)同一个数(或式子)不等号的方向不变.不等式组是否也具有类似的性质?请完成下列填空(填“>”或“<”),探索归纳得到一般的关系式:(1)、已知可得5+2 3+1,已知可得﹣5﹣2 ﹣3﹣1;
已知可得﹣2+1 3+4,…,一般地,如果 , 那么a+c b+d.
(2)、应用不等式的性质证明上述关系式.22. 某校准备组织290名学生进行野外考察活动,行李件数比学生人数的一半还少45.学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车最多能载30人和20件行李.(1)、求行李有多少件?(2)、现计划租用甲种汽车x辆,请你帮学校设计所有可能的租车方案.(3)、如果甲、乙两种汽车每辆的租车费分别是2000元、1800元,请你选择最省钱的一种租车方案,并求出至少的费用是多少元.