广东省茂名市电白区2018-2019学年高二下学期期末数学（文)试题

试卷更新日期：2020-06-24 类型：期末考试

进入出卷网下载

一、单选题

1. 若集合 $Α = {x | - 5 < x < 2}$ ， $Β = {x | - 3 < x < 3}$ ，则 $Α \cap Β =$ （）

A、 ${x | - 3 < x < 2}$ B、 ${x | - 5 < x < 2}$ C、 ${x | - 3 < x < 3}$ D、 ${x | - 5 < x < 3}$

查看试题解析
2. $\frac{3 + i}{1 + i} =$ （）

A、 $2 - i$ B、 $2 + i$ C、 $1 + 2 i$ D、 $1 - 2 i$

查看试题解析
3. 命题“∀x∈R，∃n∈N^* ，使得n≥x²”的否定形式是（）

A、∀x∈R，∃n∈N^* ，使得n＜x² B、∀x∈R，∀n∈N^* ，使得n＜x² C、∃x∈R，∃n∈N^* ，使得n＜x² D、∃x∈R，∀n∈N^* ，使得n＜x²

查看试题解析
4. 已知函数 $f (x) = 3^{x} - {(\frac{1}{3})}^{x}$ ，则 $f (x)$ （）

A、是奇函数，且在R上是增函数 B、是偶函数，且在R上是增函数 C、是奇函数，且在R上是减函数 D、是偶函数，且在R上是减函数

查看试题解析
5. 已知双曲线 $\frac{x^{2}}{a {}^{2}} - \frac{y^{2}}{3} = 1 (a > 0)$ 的离心率为2，则 $a =$ （）

A、2 B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、1

查看试题解析
6.
某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图，图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃，下面叙述不正确的是（　　）

A、各月的平均最低气温都在0℃以上 B、七月的平均温差比一月的平均温差大 C、三月和十一月的平均最高气温基本相同 D、平均最高气温高于20℃的月份有5个

查看试题解析
7. 函数 f(x)=(x−3)e^x 的单调递增区间是（）

A、 $(- \infty ， 2)$ B、 $(0 ， 3)$ C、 $(1 ， 4)$ D、 $(2 ， + \infty)$

查看试题解析
8. 执行如图所示的程序框图，如果输入n=3，输出的S=（）

A、 $\frac{6}{7}$ B、 $\frac{3}{7}$ C、 $\frac{8}{9}$ D、 $\frac{4}{9}$

查看试题解析
9. 已知函数 $f (x) = 2 {cos}^{2} x - {sin}^{2} x + 2$ ，则（）

A、 $f (x)$ 的最小正周期为 $π$ ，最大值为3 B、 $f (x)$ 的最小正周期为 $π$ ，最大值为4 C、 $f (x)$ 的最小正周期为 $2 π$ ，最大值为3 D、 $f (x)$ 的最小正周期为 $2 π$ ，最大值为4

查看试题解析
10. 设在 $Δ A B C$ 中,角 $A ， B, C$ 所对的边分别为 $a ， b, c$ , 若 $b \cos C + c \cos B = a \sin A$ , 则 $Δ A B C$ 的形状为（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不确定

查看试题解析
11. 一个四面体的三视图如图所示，则该四面体的表面积是（）

A、 $1 + \sqrt{3}$ B、 $2 + \sqrt{3}$ C、 $1 + 2 \sqrt{2}$ D、 $2 \sqrt{2}$

查看试题解析
12. 已知函数 $f (x) = x^{2} - 2 x + a (e^{x - 1} + e^{- x + 1})$ 有唯一零点，则a=（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析

二、填空题

13. 已知函数 $f (x) = {\begin{array}{l} x (x + 4), x \geq 0 \\ x (x - 4), x < 0 \end{array}$ ，则 $f (1) + f (- 3) =$ ．

查看试题解析
14. 已知向量 $\vec{a} = (- 1, 2)$ ， $\vec{b} = (m, 1)$ .若向量 $\vec{a} + \vec{b}$ 与 $\vec{a}$ 垂直，则 $m =$ .

查看试题解析
15. 若x，y满足约束条件 ${\begin{matrix} x - y + 1 \geq 0 ， \\ x + y - 3 \geq 0 ， \\ x - 3 \leq 0 ， \end{matrix}$ 则z=x−2y的最小值为.

查看试题解析
16.
如图，在圆柱O₁O₂内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O₁O₂的体积为V₁ ，球O的体积为V₂ ，则 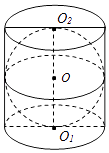$\frac{V_{1}}{V_{2}}$ 的值是．

查看试题解析

三、解答题

17. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，已知 $a_{1} = - 7$ ， $S_{3} = - 15$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求 $S_{n}$ ，并求 $S_{n}$ 的最小值．

查看试题解析
18. 为了比较两种治疗失眠症的药（分别成为A药，B药）的疗效，随机地选取20位患者服用A药，20位患者服用B药，这40位患者服用一段时间后，记录他们日平均增加的睡眠时间（单位：h）实验的观测结果如下：
服用A药的20位患者日平均增加的睡眠时间：

0.61.22.71.52.81.82.22.33.23.5

2.52.61.22.71.52.93.03.12.32.4

服用B药的20位患者日平均增加的睡眠时间：

3.21.71.90.80.92.41.22.61.31.4

1.60.51.80.62.11.12.51.22.70.5

(1)、分别计算两组数据的平均数，从计算结果来看，哪种药的效果好？

(2)、完成茎叶图，从茎叶图来看，哪种药疗效更好？

查看试题解析
19. 如图，四棱锥P−ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

（Ⅰ）证明MN∥平面PAB；

（Ⅱ）求直线AN与平面PMN所成角的正弦值.

查看试题解析
20. 已知点A(0，－2)，椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的离心率为 $\frac{\sqrt{3}}{2}$ ，F是椭圆E的右焦点，直线AF的斜率为 $\frac{2 \sqrt{3}}{3}$ ，O为坐标原点.

(1)、求E的方程；

(2)、设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

查看试题解析
21. 已知函数 $f (x) = \frac{1}{3} x^{3} - a (x^{2} + x + 1)$

(1)、若a=3，求 $f (x)$ 的单调区间

(2)、证明： $f (x)$ 只有一个零点

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，曲线 $C_{1}$ 的参数方程为 ${\begin{matrix} x = 2 c o s φ \\ y = s i n φ \end{matrix}$ （ $φ$ 为参数），在以 $O$ 为极点， $x$ 轴的正半轴为极轴的极坐标系中，曲线 $C_{2}$ 是圆心为 $(3, \frac{π}{2})$ ，半径为1的圆.

(1)、求曲线 $C_{1}$ ， $C_{2}$ 的直角坐标方程；

(2)、设 $M$ 为曲线 $C_{1}$ 上的点， $N$ 为曲线 $C_{2}$ 上的点，求 $| M N |$ 的取值范围.

查看试题解析
23. 已知函数 $f (x) = | x + 1 | - 2 | x - a |, a > 0$ .

(1)、当 $a = 1$ 时，求不等式 $f (x) > 1$ 的解集；

(2)、若 $f (x)$ 的图象与 $x$ 轴围成的三角形面积大于6，求 $a$ 的取值范围.

查看试题解析