广东省茂名市电白区2018-2019学年高二下学期理数期末考试试卷

试卷更新日期：2020-06-24 类型：期末考试

进入出卷网下载

一、单选题

1. 若复数 $z = \frac{2}{1 - i}$ ，其中i为虚数单位，则 $\bar{z}$ =（）

A、1+i B、1−i C、−1+i D、−1−i

查看试题解析
2. 设集合 $A = {x | x^{2} - 2 x < 0} ， B = {x | 1 \leq x \leq 4}$ ，则 $A \cap B =$ （）

A、 $(0 ， 2]$ B、 $(1 ， 2)$ C、 $[1 ， 2)$ D、 $(1 ， 4)$

查看试题解析
3. 命题“∀x∈R，∃n∈N^* ，使得n≥x²”的否定形式是（）

A、∀x∈R，∃n∈N^* ，使得n＜x² B、∀x∈R，∀n∈N^* ，使得n＜x² C、∃x∈R，∃n∈N^* ，使得n＜x² D、∃x∈R，∀n∈N^* ，使得n＜x²

查看试题解析
4. 如图，在平行四边形ABCD中，E为DC边的中点，且 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ ，则 $\vec{B E} =$ （）

A、 $\vec{b} - \frac{1}{2} \vec{a}$ B、 $\vec{b} + \frac{1}{2} \vec{a}$ C、 $\vec{a} + \frac{1}{2} \vec{b}$ D、 $\vec{a} - \frac{1}{2} \vec{b}$

查看试题解析
5. 执行如图所示的程序框图，如果输入n=3，输出的S=（）

A、 $\frac{6}{7}$ B、 $\frac{3}{7}$ C、 $\frac{8}{9}$ D、 $\frac{4}{9}$

查看试题解析
6.
某旅游城市为向游客介绍本地的气温情况，绘制了一年中各月平均最高气温和平均最低气温的雷达图，图中A点表示十月的平均最高气温约为15℃，B点表示四月的平均最低气温约为5℃，下面叙述不正确的是（　　）

A、各月的平均最低气温都在0℃以上 B、七月的平均温差比一月的平均温差大 C、三月和十一月的平均最高气温基本相同 D、平均最高气温高于20℃的月份有5个

查看试题解析
7. 函数 $f (x) = \frac{ln x - 2 x}{x}$ 的图象在点 $(1 ， - 2)$ 处的切线方程为 $($ $)$

A、 $2 x - y - 4 = 0$ B、 $2 x + y = 0$ C、 $x - y - 3 = 0$ D、 $x + y + 1 = 0$

查看试题解析
8. 已知等差数列{a_n}前9项的和为27，a₁₀=8，则a₁₀₀=（）

A、100 B、99 C、98 D、97

查看试题解析
9. 已知函数 $f (x) = 2 {cos}^{2} x - {sin}^{2} x + 2$ ，则（）

A、 $f (x)$ 的最小正周期为 $π$ ，最大值为3 B、 $f (x)$ 的最小正周期为 $π$ ，最大值为4 C、 $f (x)$ 的最小正周期为 $2 π$ ，最大值为3 D、 $f (x)$ 的最小正周期为 $2 π$ ，最大值为4

查看试题解析
10. 某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（）

A、1 B、2 C、3 D、4

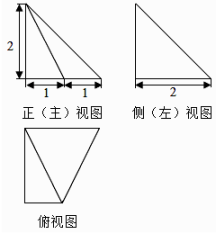查看试题解析
11. 设 $A ， B ， C ， D$ 是同一个半径为4的球的球面上四点， $△ A B C$ 为等边三角形且其面积为 $9 \sqrt{3}$ ，则三棱锥 $D - A B C$ 体积的最大值为（）

A、 $12 \sqrt{3}$ B、 $18 \sqrt{3}$ C、 $24 \sqrt{3}$ D、 $54 \sqrt{3}$

查看试题解析
12. 已知点 $M (- 1 ， 0)$ 和 $N (1 ， 0)$ ，若某直线上存在点P，使得 $| P M | + | P N | = 4$ ，则称该直线为“椭型直线”，现有下列直线：
① $x - 2 y + 6 = 0$ ； ② $x - y = 0$ ； ③ $2 x - y + 1 = 0$ ； ④ $x + y - 3 = 0$ ．

其中是“椭型直线”的是（）

A、①③ B、①② C、②③ D、③④

查看试题解析

二、填空题

13. 已知函数 $f (x) = {\begin{array}{l} x (x + 4) ， x \geq 0 \\ x (x - 4) ， x < 0 \end{array}$ ，则 $f (1) + f (- 3) =$ ．

查看试题解析
14. 若x，y满足约束条件 ${\begin{matrix} x - y + 1 \geq 0 ， \\ x + y - 3 \geq 0 ， \\ x - 3 \leq 0 ， \end{matrix}$ 则z=x−2y的最小值为.

查看试题解析
15. 若 $($ ax²+ $\frac{1}{\sqrt{x}})^{5}$ 的展开式中x⁵的系数是—80，则实数a=.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} \ln (- x) ， x < 0 \\ e^{x} + e^{2 - x} - a ， x \geq 0 \end{array}$ ，若 $f (x)$ 的所有零点之和为1，则实数 $a$ 的取值范围为．

查看试题解析

三、解答题

17. 在 $Δ A B C$ 中， $∠ A = 60^{\circ}$ ， $c = \frac{3}{7} a .$

(1)、求 $sin C$ 的值；

(2)、若 $a = 7$ ，求 $Δ A B C$ 的面积．

查看试题解析
18. 已知等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，各项为正的等比数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ， $a_{1} = - 1$ ， $b_{1} = 1$ ， $a_{2} + b_{2} = 2$ .

(1)、若 $a_{3} + b_{3} = 5$ ，求 ${b_{n}}$ 的通项公式；

(2)、若 $T_{3} = 21$ ，求 $S_{3}$

查看试题解析

19. 电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图，将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”．

(1)、根据已知条件完成下面的2×2列联表，并据此资料判断是否在犯错误的概率不超过

0.10

的前提下认为"体育迷"与性别有关．

性别	非体育迷	体育迷	总计
男
女		10	55
总计

下面的临界值表供参考：

3	0.15	0.10	0.05	0.25	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

(参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + a)}$ ，其中 $n = a + b + c + d$ )

(2)、将上述调查所得到的频率视为概率，现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为X，若每次抽取的结果是相互独立的，求X的分布列､期望

E (X)

和方差

D (X)

．

查看试题解析

20. 如图，四棱锥P−ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

（Ⅰ）证明MN∥平面PAB；

（Ⅱ）求直线AN与平面PMN所成角的正弦值.

查看试题解析
21. 已知点A(0，－2)，椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ (a>b>0)的离心率为 $\frac{\sqrt{3}}{2}$ ，F是椭圆E的右焦点，直线AF的斜率为 $\frac{2 \sqrt{3}}{3}$ ，O为坐标原点.

(1)、求E的方程；

(2)、设过点A的动直线l与E相交于P，Q两点.当△OPQ的面积最大时，求l的方程.

查看试题解析
22. 已知函数 $f (x) = \frac{e^{x} - a}{x}$ ， $g (x) = a \ln x + a$ .

(1)、 $a = 1$ 时，求 $F (x) = f (x) - g (x)$ 的单调区间；

(2)、若 $x > 1$ 时，函数 $y = f (x)$ 的图象总在函数 $y = g (x)$ 的图象的上方，求实数的取值范围.

查看试题解析