深圳市2020年初中数学八年级下册期末模拟试卷
试卷更新日期:2020-06-24 类型:期末考试
一、单选题
-
1. 如图,在△ABC 中,∠BAC=72°,∠C=36°,∠BAC 的平分线 AD 交 BC 于 D, 则图中有等腰三角形( )
 A、0 个 B、1 个 C、2 个 D、3 个2. 下列标志既是轴对称图形又是中心对称图形的是( )A、
A、0 个 B、1 个 C、2 个 D、3 个2. 下列标志既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 如果 a<b , 那么下列不等式成立的是( )A、a﹣b>0 B、a﹣3>b﹣3 C、2a>2b D、﹣3a>﹣3b4. 下列分解因式正确的是( )A、x2﹣3x+1=x(x﹣3)+1 B、a2b﹣2ab+b=b(a﹣1)2 C、4a2﹣1=(4a+1)(4a﹣1) D、(x﹣y)2=x2﹣2xy+y25. 分式 有意义,则x的取值范围是( )A、x>1 B、x=1 C、x≠1 D、x<16. 不等式组 的解集在数轴上表示正确的是( )A、
3. 如果 a<b , 那么下列不等式成立的是( )A、a﹣b>0 B、a﹣3>b﹣3 C、2a>2b D、﹣3a>﹣3b4. 下列分解因式正确的是( )A、x2﹣3x+1=x(x﹣3)+1 B、a2b﹣2ab+b=b(a﹣1)2 C、4a2﹣1=(4a+1)(4a﹣1) D、(x﹣y)2=x2﹣2xy+y25. 分式 有意义,则x的取值范围是( )A、x>1 B、x=1 C、x≠1 D、x<16. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、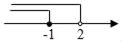 C、
C、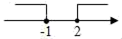 D、
D、 7. 如图,点 的坐标分别为 、 ,将 沿 轴向右平移,得到三角形 ,已知 ,则点 的坐标为( )
7. 如图,点 的坐标分别为 、 ,将 沿 轴向右平移,得到三角形 ,已知 ,则点 的坐标为( ) A、 B、 C、 D、8. 如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:
A、 B、 C、 D、8. 如图,已知△ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:①分别以A、C为圆心,以大于 AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
则四边形ADCE的周长为( )
 A、10 B、20 C、12 D、249. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )
A、10 B、20 C、12 D、249. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为( )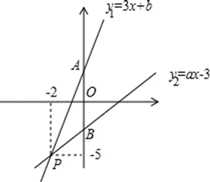 A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 一把5m长的梯子AB斜靠在墙上,梯子倾斜角α的正切值为 ,考虑安全问题,现要求将梯子的倾斜角改为30°,则梯子下滑的距离AA'的长度是( )
A、x>﹣2 B、x<﹣2 C、x>﹣5 D、x<﹣510. 一把5m长的梯子AB斜靠在墙上,梯子倾斜角α的正切值为 ,考虑安全问题,现要求将梯子的倾斜角改为30°,则梯子下滑的距离AA'的长度是( )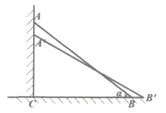 A、 m B、 m C、 m D、 m11. 下列四个命题:①有两边及其中一边的对角对应相等的两个三角形全等;②三角形的一条中线把三角形分成面积相等的两部分:③若 ,则 >0:④点P(1,2)关于原点的对称点坐标为P(-1,-2);其中真命题的是( )A、①、② B、②、④ C、③、④ D、①、③12. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …按照此规律继续下去,则S2016的值为( )
A、 m B、 m C、 m D、 m11. 下列四个命题:①有两边及其中一边的对角对应相等的两个三角形全等;②三角形的一条中线把三角形分成面积相等的两部分:③若 ,则 >0:④点P(1,2)关于原点的对称点坐标为P(-1,-2);其中真命题的是( )A、①、② B、②、④ C、③、④ D、①、③12. 如图,正方形ABCD的边长为2,其面积标记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2 , …按照此规律继续下去,则S2016的值为( )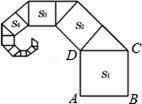
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如果x2﹣x﹣1=0,那么代数式2x2﹣2x﹣3的值是 .14. 化简:( )•(x2﹣1)=.15. 不等式的解集是 .
16. 如图,在△ABC 中,D、E、F 分别是 BC、AC、AB 边的中点,AH⊥BC 于 H , HE=8,则线段DF的长是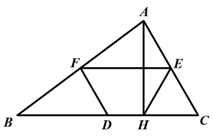
三、解答题
-
17. 因式分解:(1)、 ;(2)、 .18. 化简:( ﹣ )÷ .19. 解方程: .20. △ABC在平面直角坐标系中的位置如图所示,A、
B、C三点在格点(小正方形的顶点)上.
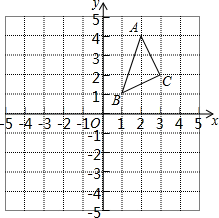 (1)、作出△ABC关于x轴对称的△A1B1C1 , 写出点A1、B1、C1的坐标;(2)、求△ABC的面积.21. 如图,平行四边形 ABCD 的对角线 AC、BD 交于 O 点,AE∥BD,∠AED=∠AOD,连接 OE.
(1)、作出△ABC关于x轴对称的△A1B1C1 , 写出点A1、B1、C1的坐标;(2)、求△ABC的面积.21. 如图,平行四边形 ABCD 的对角线 AC、BD 交于 O 点,AE∥BD,∠AED=∠AOD,连接 OE. (1)、求证:AE=OB;(2)、求证:四边形 CDEO 是平行四边形.22. 随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加,据统计,某小区2016年底拥有家庭电动自行车125辆,2018年底家庭电动自行车的拥有量达到180辆.(1)、若该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率相同,按照这个增长速度该小区2019年底家庭电动自行车将达到多少辆?(2)、为了缓解停车矛盾,该小区决定再建40个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个,考虑到实际因素,该小区计划投资费用不超过20000元,则该小区最多可建室内车位多少个?23. 如图所示,在矩形ABCD中,AB=CD=5,BC=AD=3.
(1)、求证:AE=OB;(2)、求证:四边形 CDEO 是平行四边形.22. 随着人们环保意识的不断增强,我市家庭电动自行车的拥有量逐年增加,据统计,某小区2016年底拥有家庭电动自行车125辆,2018年底家庭电动自行车的拥有量达到180辆.(1)、若该小区2016年底到2018年底家庭电动自行车拥有量的平均增长率相同,按照这个增长速度该小区2019年底家庭电动自行车将达到多少辆?(2)、为了缓解停车矛盾,该小区决定再建40个停车位,据测算,建造费用分别为室内车位1000元/个,露天车位200元/个,考虑到实际因素,该小区计划投资费用不超过20000元,则该小区最多可建室内车位多少个?23. 如图所示,在矩形ABCD中,AB=CD=5,BC=AD=3. (1)、如图①,E、F分别为CD、AB边上的点,将矩形ABCD沿EF翻折,使点A与点C重合,设CE=x , 则DE=(用含x的代数式表示),CD′=AD=3,在Rt△CD′E中,利用勾股定理列方程,可求得CE=.(2)、如图②,将△ABD沿BD翻折至△A′BD,若A′B交CD于点E,求此时CE的长;(3)、如图③,P为AD边上的一点,将△ABP沿BP翻折至△A′BP,A′B、A′P分别交CD边于E. F,且DF=A′F,请直接写出此时CE的长.
(1)、如图①,E、F分别为CD、AB边上的点,将矩形ABCD沿EF翻折,使点A与点C重合,设CE=x , 则DE=(用含x的代数式表示),CD′=AD=3,在Rt△CD′E中,利用勾股定理列方程,可求得CE=.(2)、如图②,将△ABD沿BD翻折至△A′BD,若A′B交CD于点E,求此时CE的长;(3)、如图③,P为AD边上的一点,将△ABP沿BP翻折至△A′BP,A′B、A′P分别交CD边于E. F,且DF=A′F,请直接写出此时CE的长.