深圳市2020年初中数学七年级下册期末模拟试卷
试卷更新日期:2020-06-24 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图的是( )A、
 B、
B、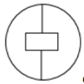 C、
C、 D、
D、 2. 肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )A、 B、 C、 D、3. 下列运算结果正确的是( )A、 B、 C、 D、4. 下列四个图形中,能推出∠1与∠2相等的是( )A、
2. 肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )A、 B、 C、 D、3. 下列运算结果正确的是( )A、 B、 C、 D、4. 下列四个图形中,能推出∠1与∠2相等的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,若AB∥CD,CD∥EF,那么∠BCE=( )
5. 如图,若AB∥CD,CD∥EF,那么∠BCE=( )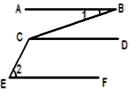 A、∠1+∠2 B、∠2-∠1 C、180°-∠1+∠2 D、180°-∠2+∠16. 一个布袋里装有2个红球,3个黄球和5个白球,除颜色外其它都相同,搅匀后任意摸出一个球,是白球的概率为( )A、 B、 C、 D、7. 下列是利用了三角形的稳定性的有( )
A、∠1+∠2 B、∠2-∠1 C、180°-∠1+∠2 D、180°-∠2+∠16. 一个布袋里装有2个红球,3个黄球和5个白球,除颜色外其它都相同,搅匀后任意摸出一个球,是白球的概率为( )A、 B、 C、 D、7. 下列是利用了三角形的稳定性的有( )①自行车的三角形车架:②校门口的自动伸缩栅栏门:③照相机的三脚架:④长方形门框的斜拉条
A、1个 B、2个 C、3个 D、4个8. 下列事件中,是必然事件的是( )A、三条线段可以组成一个三角形 B、400人中有两个人的生日在同一天 C、早上的太阳从西方升起 D、打开电视机,它正在播放动画片9. 如图, 中, , 是 的中线,E是 的中点,连接 ,若 , ,则 ( )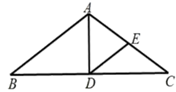 A、 B、 C、 D、10. 如图,多边形ABCDEFG中, ,则 的值为( )
A、 B、 C、 D、10. 如图,多边形ABCDEFG中, ,则 的值为( )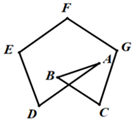 A、 B、 C、 D、11. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为 ,剩下的水量为 .下面能反映 与 之间的关系的大致图象是( )A、
A、 B、 C、 D、11. 一水池放水,先用一台抽水机工作一段时间后停止,然后再调来一台同型号抽水机,两台抽水机同时工作直到抽干.设从开始工作的时间为 ,剩下的水量为 .下面能反映 与 之间的关系的大致图象是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,AB⊥BC,OB=OC,CD⊥BC,点A,O,D在一条直线上,通过测量CD的长可知小河的宽AB.由此判定△AOB≌△DOC的依据是( )
12. 如图,AB⊥BC,OB=OC,CD⊥BC,点A,O,D在一条直线上,通过测量CD的长可知小河的宽AB.由此判定△AOB≌△DOC的依据是( )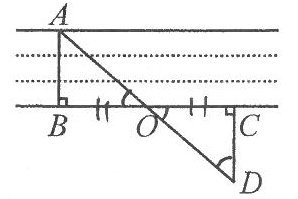 A、SAS或SSA B、ASA或AAS C、SAS或ASA D、SSS或AAS
A、SAS或SSA B、ASA或AAS C、SAS或ASA D、SSS或AAS二、填空题
-
13. 如图,把一根直尺与一块三角尺如图放置,若∠1=55°,则∠2的度数为.
 14. 如图直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为 .
14. 如图直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为 . 15. 如图,直线 ,AE平分 ,AE与CD相交于点后, ,则 的度数是
15. 如图,直线 ,AE平分 ,AE与CD相交于点后, ,则 的度数是 16. 将一张长方形的纸对折,如图,可得到一条折痕(图中虚线),连续对折,对折时每次折痕与上次的折痕保持平行,连续对折3次后,可以得7条折痕,连续对折 次后,可以得到条折痕.
16. 将一张长方形的纸对折,如图,可得到一条折痕(图中虚线),连续对折,对折时每次折痕与上次的折痕保持平行,连续对折3次后,可以得7条折痕,连续对折 次后,可以得到条折痕.
三、解答题
-
17. 计算下列各题(1)、(﹣ab)3(5a2b﹣4ab2);(2)、(2x﹣1)(4x2+2x+1)(3)、求5x(2x+1)﹣(2x+3)(5x﹣1)的值,其中x=12.18. 先化简,再求值: ,其中 , .19. 暑假将至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动。活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止).大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
奖次
特等奖
一等奖
二等奖
三等奖
不获奖
圆心角
10°
30°
80°
120°
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆, 一等奖:双肩背包一个, 二等奖:洗衣液一桶 , 三等奖:抽纸一盒.根据以上信息,解答下列问题
(1)、求不获奖的扇形区域圆心角度数是多少?(2)、求获得双肩背包的概率是多少?(3)、甲顾客购物520元,求他获奖的概率是多少?20. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: (1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?21. 推理填空
(1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、我们认为骑单车的速度超过 300 米/分就超过了安全限度.问:在整个上学途中哪个时间段小明的骑车速度最快,最快速度为多少,在安全限度内吗?21. 推理填空如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBC=∠F,求证:CE∥DF.请完成下面的解题过程.

∵BD平分∠ABC,CE平分∠ACB(已知)
∴∠DBC= ∠ , ∠ECB= ∠(角平分线的定义)
又∵∠ABC=∠ACB(已知)
∴∠=∠.
又∵∠=∠(已知)
∴∠F=∠
∴CE∥DF.
22. 在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:功率
使用寿命
价格
普通白帜灯
100瓦(即0.1千瓦)
2000小时
3元/盏
优质节能灯
20瓦(即0.02千瓦)
4000小时
35元/盏
已知这两种灯的照明效果一样,小明家所在地的电价是每度0.5元.
(注:用电度数=功率(千瓦)×时间(小时),费用=灯的售价+电费)
请你解决以下问题:
(1)、如果选用一盏普通白炽灯照明1000小时,那么它的费用是多少?(2)、在白炽灯的使用寿命内,设照明时间为x小时,请用含x的式子分别表示用一盏白炽灯的费用和一盏节能灯的费用;(3)、照明多少小时时,使用这两种灯的费用相等?(4)、如果计划照明4000小时,购买哪一种灯更省钱?请你通过计算说明理由.23. 如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC. (1)、∠D和∠ECB相等吗?若相等,请说明理由;(2)、△ADC≌△BCE吗?若全等,请说明理由;(3)、能否找到与AB+AD相等的线段,并说明理由。
(1)、∠D和∠ECB相等吗?若相等,请说明理由;(2)、△ADC≌△BCE吗?若全等,请说明理由;(3)、能否找到与AB+AD相等的线段,并说明理由。