吉林2020年初中数学七年级下册期末模拟试卷（一）
试卷更新日期：2020-06-24 类型：期末考试
一、单选题
-
1. 下列图案中，既可以看作是轴对称图形，也可以看作是中心对称图形的是（ ）A、
B、
C、
D、
2. 如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移得到四边形A1B1C1D1 ， 已知A（-3，5)，B(-4，3)，A1(3，3)，则B1的坐标为（ ）
A、(1，2) B、(1，4) C、(2，1) D、(4，1)3. 如图，在△ABC中，∠B＝50°，点D在BC上，且AB＝BD，AD＝CD，则∠C的度数为（ ）
A、30° B、32.5° C、45° D、60°4. 用下列同一种正多边形地砖铺地面，能恰好铺满地面的是（ ）A、正五边形 B、正七边形 C、正六边形 D、正八边形5. 如图，将三角形AOB绕点O按逆时针方向旋转45°后得到三角形A'OB'，若∠AOB=21°，则∠AOB′的度数是（ ）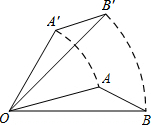
A、21° B、24° C、45° D、66°6. 已知三角形的三边长分别为2、x、3，则x可能是（ ）A、5 B、1 C、6 D、47. 如图，在四边形 中， .不能判定 的条件是（ ）
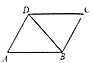A、 B、 C、 D、8. 如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②∠ADC＝∠GCD；③CA平分∠BCG；④∠DFB＝ ∠CGE.其中正确的结论是（ ）
A、②③ B、①②④ C、①③④ D、①②③④二、填空题
-
9. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1＝30°，∠2＝20°，则∠B＝.
10. 某校组织学生参加植树活动，已知七年1班有28人在甲处植树，七年2班有21人在乙处植树．现调七年3班20人去支援，使在甲处植树的人数是乙处人数的2倍，问应调往甲处多少人?设应调往甲处x人，根据题意可列得方程为：。11. 如图所示的花朵图案，至少要旋转度后，才能与原来的图形重合．
12. 如图，△ABC中，AB=AC，∠A=40°，DE垂直平分AC交AB于E，则∠BCE=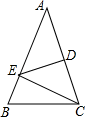
13. 若关于x、y的二元一次方程组 的解满足x+y＞0，则m 的取值范是 ．14. 如图 ，△ACE ≌△DBF ，如果∠E=∠F ，AD=10 ，BC=2 ，那么线段AB的长是 ．
三、综合题
-
15. 解不等式组： .16. 在等边三角形 中，点 从点 出发沿射线 运动，同时点 从点 出发沿线段 的延长线运动， 、 两点运动的速度相同， 与直线 相交于点 .
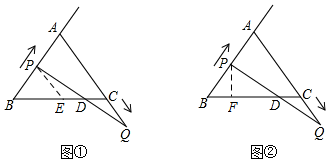(1)、如图①，过点 作 交 于点 ，求证： .(2)、如图②，过点 作直线 的垂线，垂足为 .①当点 在线段 上运动时，求证： .
②当点 在线段 延长线上运动时，直接写出 、 与 之间的数量关系.
17. 如图，在 内， 是 边上的高， 平分 交 边于 ， ， ，求 的度数.
18. 疫情期间，学校为了学生在班级将生活垃圾和废弃口罩分类丢弃，准备购买A,B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需270元，购买2个A型垃圾箱比购买3个B型垃圾箱少用80元.求每个A型垃圾箱和B型垃圾箱各多少元？学校购买A型垃圾桶8个，B型垃圾桶16个，共花费多少元？19. 如图， ， ， ，求证： .
20. 如图，在正方形网格上有一个三角形 ABC(三个顶点均在格点上)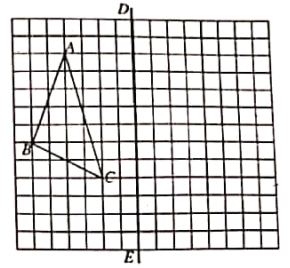
(1)、画出△ABC 关于直线DE对称的△A1B1C1(其中点A 与点 A1对应，点B与点B1对应，点C 与点C1对应)(2)、若每个小正方形的边长都是1，计算△A1B1C1的面积21.已知，如图，延长
的各边，使得 
， 
，顺次连接 
，得到 
为等边三角形．求证：
(1)、
(2)、 为等边三角形．22. 某地新建了一个企业，每月将生产1 960 t污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：
已知商家售出的2台A型、3台B型污水处理器的总价为44万元，售出的1台A型、4台B型污水处理器的总价为42万元．
(1)、求每台A型、B型污水处理器的价格；(2)、为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么至少要支付多少钱？23. 如图，点O为直线AB上一点，过点O作射线OC，使∠BOC＝135°，将一个含45°角的直角三角尺的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边都在直线AB的下方．
(1)、将图1中的三角尺绕着点O逆时针旋转90°，如图2所示，此时∠BOM＝度（答案直接填写在答题卡的横线上）；在图2中，OM是否平分∠CON?请说明理由；(2)、紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示，使得ON在∠AOC的内部，请探究：∠AOM与∠CON之间的数量关系，并说明理由；(3)、将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，请你直接写出t的值为多少．24. 解方程组：(1)、(2)、 .