吉林2020年初中数学八年级下册期末模拟试卷(二)
试卷更新日期:2020-06-24 类型:期末考试
一、单选题
-
1. 二次根式 中x的取值范围是( )A、X>3 B、x≥3 C、x≤3 D、x<32. 在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点B,则点B所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 甲、乙、丙、丁四位选手各射击10次,每人的平均成绩都是9.3环,方差如表:
选手
甲
乙
丙
丁
方差(环2)
0.035
0.016
0.022
0.025
则这四个人种成绩发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁4. 如图,以两条直线l1 , l2的交点坐标为解的方程组是( ) A、 B、 C、 D、5. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③△PFD∽△PDB④DP2=PH·PC其中正确的有( )
A、 B、 C、 D、5. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③△PFD∽△PDB④DP2=PH·PC其中正确的有( )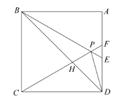 A、①②③④ B、②③ C、①②④ D、①③6. 如图,四边形 是菱形, ,点 从 点出发,沿 运动,过点 作直线 的垂线,垂足为 ,设点 运动的路程为 , 的面积为 ,则下列图象能正确反映 与 之间的函数关系的是( ).
A、①②③④ B、②③ C、①②④ D、①③6. 如图,四边形 是菱形, ,点 从 点出发,沿 运动,过点 作直线 的垂线,垂足为 ,设点 运动的路程为 , 的面积为 ,则下列图象能正确反映 与 之间的函数关系的是( ). A、
A、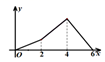 B、
B、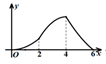 C、
C、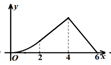 D、
D、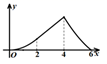 7. 下列四个命题中错误的是( )A、对角线相等的菱形是正方形 B、有两边相等的平行四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分的四边形是平行四边形8. 如图,在平面直角坐标系xOy中, 四边形ABCD是矩形,点A的坐标为(2,0),点B的坐标为(0,4),顶点C在反比例函数y= 的图像上,若 AD:AB=1:2,则k的值是( )
7. 下列四个命题中错误的是( )A、对角线相等的菱形是正方形 B、有两边相等的平行四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分的四边形是平行四边形8. 如图,在平面直角坐标系xOy中, 四边形ABCD是矩形,点A的坐标为(2,0),点B的坐标为(0,4),顶点C在反比例函数y= 的图像上,若 AD:AB=1:2,则k的值是( ) A、8 B、10 C、12 D、6
A、8 B、10 C、12 D、6二、填空题
-
9. 最简二次根式 与 是同类二次根式,则a= , b=.10. 某中学规定:学生的学期体育综合成绩满分为100分,其中,期中考试成绩占30%,期末考试成绩占70%,小宁这个学期的期中、期末成绩(百分制)分别是80分、90分,则小宁这个学期的体育综合成绩是分11. 如图所示,正比例函数y1=k1x(k1≠0)的图像与反比例函数y2= (k2≠0)的图像相交于A、B两点,其中A的横坐标为2,当y1<y2<0时,则x的取值范围是.
 12. 如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F,则△AFC的面积为.
12. 如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F,则△AFC的面积为.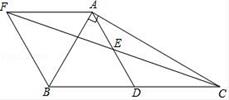 13. 如图,将两条宽度为3的直尺重叠在一起,使∠ABC=60°,则四边形ABCD的面积是
13. 如图,将两条宽度为3的直尺重叠在一起,使∠ABC=60°,则四边形ABCD的面积是 14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=900 , 连结AC,若AC=10,则四边形ABCD的面积为.
14. 如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=900 , 连结AC,若AC=10,则四边形ABCD的面积为.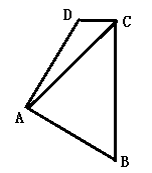
三、综合题
-
15. 计算:(1)、(2)、16. 如图,在平面直角坐标系中,正比例函数 与函数 的图象相交于点 , 轴于点B.平移直线 ,使其经过点B,得到直线l,求直线l所对应的函数表达式.
 17. 已知:如图, ABCD中,AB=5,BC=3。
17. 已知:如图, ABCD中,AB=5,BC=3。 (1)、作∠DAB的角平分线,交CD于点E(用直尺和圈规作图,不写作法,保留作图痕迹);(2)、求CE的长。18. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F
(1)、作∠DAB的角平分线,交CD于点E(用直尺和圈规作图,不写作法,保留作图痕迹);(2)、求CE的长。18. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F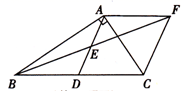 (1)、求证:△AEF≌△DEB;(2)、证明四边形ADCF是菱形;(3)、若AC=4,AB=5,求菱形ADCFD 的面积.19. 已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)、求证:△AEF≌△DEB;(2)、证明四边形ADCF是菱形;(3)、若AC=4,AB=5,求菱形ADCFD 的面积.19. 已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC. (1)、如图1,求证:四边形ADCE是矩形;(2)、如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.20. 为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
(1)、如图1,求证:四边形ADCE是矩形;(2)、如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.20. 为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:
随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲
91
89
77
86
71
31
97
93
72
91
81
92
85
85
95
88
88
90
44
91
乙
84
93
66
69
76
87
77
82
85
88
90
88
67
88
91
96
68
97
59
88
整理、描述数据:
(1)、按如下数据段整理、描述这两组数据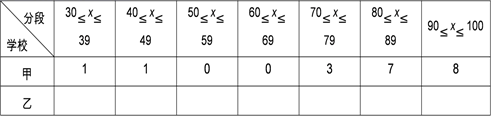 (2)、两组数据的平均数、中位数、众数、方差如下表:
(2)、两组数据的平均数、中位数、众数、方差如下表:
a经统计,表格中m的值是 .
得出结论:
b若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
c可以推断出学校学生的数学水平较高,理由为:①;② . (至少从两个不同的角度说明推断的合理性)
21. 元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象. (1)、求小黄出发0.5小时时,离家的距离;(2)、求出AB段的图象的函数解析式;(3)、小黄出发1.5小时时,离目的地还有多少千米?22. 如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE。
(1)、求小黄出发0.5小时时,离家的距离;(2)、求出AB段的图象的函数解析式;(3)、小黄出发1.5小时时,离目的地还有多少千米?22. 如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE。 (1)、求证:F为BC中点。(2)、若OB⊥AC,OF=1,求平行四边形ABCD的周长。23. 已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
(1)、求证:F为BC中点。(2)、若OB⊥AC,OF=1,求平行四边形ABCD的周长。23. 已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°. (1)、如图1,求证:CD=DE;(2)、如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系;(3)、如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.24. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限内,BC在x轴的正半轴上(B在C的右侧),AB= ,∠ACB=30°,△ADC与△ABC关于AC所在的直线对称,且函数y= (k>0)的图象过点D.
(1)、如图1,求证:CD=DE;(2)、如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系;(3)、如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.24. 如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限内,BC在x轴的正半轴上(B在C的右侧),AB= ,∠ACB=30°,△ADC与△ABC关于AC所在的直线对称,且函数y= (k>0)的图象过点D. (1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.
(1)、当OC=2时,求k的值;(2)、如图2,若点A和点D在同一个反比例函数图象上,求OC的长;(3)、在(2)的条件下,点D与点E关于原点成中心对称,x轴上有一点F,平面内有一点G,若D、E、F、G四点构成的四边形是矩形,求F点的坐标.