吉林2020年初中数学八年级下册期末模拟试卷（一）

试卷更新日期：2020-06-24 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\frac{1}{\sqrt{x - 1}}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x < 1$ B、 $x \leq 1$ C、 $x > 1$ D、 $x \geq 1$

查看试题解析
2. 下列用科学记数法能表示成3.14×10⁴的数是（）

A、0.0314 B、3140000 C、31400 D、3140

查看试题解析
3. 学校举行图书节义卖活动，将所售款项捐给其他贫困学生.在这次义卖活动中，某班级售书情况如下图：

下列说法正确的是（）

A、该班级所售图书的总数收入是226元 B、在该班级所售图书价格组成的一组数据中，中位数是4 C、在该班级所售图书价格组成的一组数据中，众数是15 D、在该班级所售图书价格组成的一组数据中，方差是2

查看试题解析
4. 下列等式变形错误的是( ）

A、若x＝y ，则x－5＝y－5 B、若－3x＝－3y ，则x＝y C、若 $\frac{x}{a}$ ＝ $\frac{y}{a}$ ，则x＝y D、若mx＝my ，则x＝y

查看试题解析
5. 如果 $a b < 0$ ，那么点P $(a ， b)$ 所在象限为（）

A、第二象限 B、第四象限 C、第一或第三象限 D、第二或第四象限

查看试题解析
6. 在四边形 $A B C D$ 中，从以下四个条件中：① $A B / / C D$ ② $A D / / B C$ ③ $A D = B C$ ④ $∠ B = ∠ D$ ，其中任选两个能判定四边形ABCD为平行四边形的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
7. 如图所示，在平面直角坐标系中，直线y₁＝2x+4分别与x轴，y轴交于A，B两点，以线段OB为一条边向右侧作矩形OCDB，且点D在直线y₂＝﹣x+b上，若矩形OCDB的面积为20，直线y₁＝2x+4与直线y₂＝﹣x+b交于点P．则P的坐标为（）

A、（2，8） B、 $(\frac{17}{3} ， \frac{31}{3})$ C、 $(\frac{5}{3} ， \frac{22}{3})$ D、（4，12）

查看试题解析
8. 若一次函数y=2x＋m的图像与x轴相交于点A（－3，0），则m的值为（）

A、－3 B、6 C、－6 D、6或－6

查看试题解析

二、填空题

9. 已知 10^x= 2， 10^y=3 ，则 $10^{2 x - y} =$ .

查看试题解析
10. 已知关于 x 的方程 2 - $\frac{1 - k x}{x - 2} = \frac{1}{2 - x}$ 有增根，则k＝．

查看试题解析
11. 如图，在△ABC中，∠ABC＝90°，D为AB边上一点（BD＜BC），AE⊥AB，AE＝BD，连接DE交AC于F，若∠AFE＝45°，AD＝3 $\sqrt{5}$ ，CD＝5，则线段AC的长度为．

查看试题解析
12. 如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于点H，连接OH，∠CAD=35°，则∠HOB的度数为．

查看试题解析
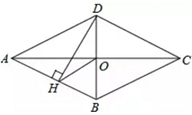13. 如图，在菱形ABCD中，AC、BD交于点O，AC＝4，菱形ABCD的面积为4 $\sqrt{5}$ ，E为AD的中点，则OE的长为．

查看试题解析
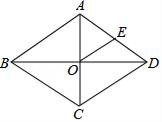14. 在平面直角坐标系中，已知 $A (2 ， 0) ， B (2 ， 2) ， C (0 ， 2)$ ，动点 $E$ 从点 $C$ 出发，以每秒1个单位的速度向下运动，动点 $F$ 从点 $A$ 出发，以每秒1个单位的速度向右运动，过点 $A$ 作 $B F$ 的平行线交 $B E$ 于点 $P$ ，当 $P O$ 的值最小时，此时 $t =$ 秒.

查看试题解析

三、综合题

15. 化简或计算：

(1)、 $\frac{a^{2} - a b}{a^{2}} \div \frac{a^{2} - b^{2}}{a b}$

(2)、 $a + 1 - \frac{a^{2}}{a - 1}$

查看试题解析
16. 甲、乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的1.2倍，两人各加工600个这种零件，甲比乙少用4天．求乙每天加工零件的个数．

查看试题解析
17. 如图，直线 $l_{1}$ 的解析式为： $y = - 3 x + 3$ ，且 $l_{1}$ 与x轴交于点D，直线 $l_{2}$ 经过点A，B，直线 $l_{1}$ ， $l_{2}$ 交于点C.

(1)、求直线 $l_{2}$ 的解析表达式；

(2)、求 $Δ A D C$ 的面积.

查看试题解析
18. 在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题.
材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一，所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的.

例：已知： $\frac{x}{x^{2} + 1} = \frac{1}{4}$ ，求代数式x²+ $\frac{1}{x^{2}}$ 的值.

解：∵ $\frac{x}{x^{2} + 1} = \frac{1}{4}$ ，∴ $\frac{x^{2} + 1}{x}$ ＝4

即 $\frac{x^{2}}{x} + \frac{1}{x}$ ＝4∴x+ $\frac{1}{x}$ ＝4∴x²+ $\frac{1}{x^{2}}$ ＝（x+ $\frac{1}{x}$ ）²﹣2＝16﹣2＝14

材料二：在解决某些连等式问题时，通常可以引入参数“k”，将连等式变成几个值为k的等式，这样就可以通过适当变形解决问题.

例：若2x＝3y＝4z，且xyz≠0，求 $\frac{x}{y + z}$ 的值.

解：令2x＝3y＝4z＝k（k≠0）

则 $x = \frac{k}{2} ， y = \frac{k}{3} ， z = \frac{k}{4} ， ∴ \frac{x}{y + z} = \frac{\frac{1}{2} k}{\frac{1}{3} k + \frac{1}{4} k} = \frac{\frac{1}{2}}{\frac{7}{12}} = \frac{6}{7}$

根据材料回答问题：

(1)、已知 $\frac{x}{x^{2} - x + 1} = \frac{1}{4}$ ，求x+ $\frac{1}{x}$ 的值.

(2)、已知 $\frac{a}{5} = \frac{b}{2} = \frac{c}{3}$ ，（abc≠0），求 $\frac{3 b + 4 c}{2 a}$ 的值.

(3)、若 $\frac{y z}{b z + c y} = \frac{z x}{c x + a z} = \frac{x y}{a y + b x} = \frac{x^{2} + y^{2} + z^{2}}{a^{2} + b^{2} + c^{2}}$ ，x≠0，y≠0，z≠0，且abc＝7，求xyz的值.

查看试题解析
19. 为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛.该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩(百分制)，并对数据(成绩)进行整理、描述和分析。下面给出了部分信息。

a.甲部门成绩的频数分布直方图如下

(数据分成6组：40≤x<50，50≤x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100)：

b.乙部门成绩如下：

乙 40 52 70 70 71 73 77 78 80 81

82 82 82 82 83 83 83 86 91 94

c.甲、乙两部门成绩的平均数、方差、中位数如下：

平均数

方差

中位数

甲

79.6

36.84

78.5

乙

77

147.2

m

d.近五年该单位参赛员工进入复赛的出线成绩如下

2014年

2015年

2016年

2017年

2018年

出线成绩(百分制)

79

81

80

81

82

根据以上信息，回答下列问题

(1)、写出表中m的值；

(2)、可以推断出选择部门参赛更好，理由为。

(3)、预估(2)中部门今年参赛进入复赛的人数为。

查看试题解析
20. 如图，矩形ABCD的对角线相交于点O ，分别过点C、D作CE∥BD、DE∥AC ， CE、DE交于点E ．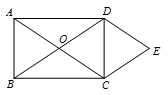

(1)、求证：四边形OCED是菱形．

(2)、将矩形ABCD改为菱形ABCD ，其余条件不变，连结OE ．若AC=10，BD=24，则OE的长为．

查看试题解析
21. 如图，已知一次函数y＝kx+b（k≠0）的图象与x轴、y轴分别交于点A、B两点，且与反比例函数y＝ $\frac{m}{x}$ 的图象在第一象限内的部分交于点C，CD垂直于x轴于点D，其中OA＝OB＝OD＝2．

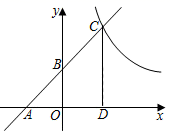(1)、直接写出点A、C的坐标；

(2)、求这两个函数的表达式；

(3)、若点P在y轴上，且S_△_ACP＝14，求点P的坐标．

查看试题解析
22. 已知，如图，在平行四边形ABCD中，BF平分 $∠ A B C$ 交AD于点F，AE $⊥$ BF于点O，交BC于点E，连接EF.

(1)、求证：四边形ABEF是菱形；

(2)、若AE=6，BF=8，CE=3，求四边形ABCD的面积.

查看试题解析
23. 某市自来水公司为限制单位用水，每月只给某单位计划内用水 3000 吨，计划内用水每吨收费 0.5元，超计划部分每吨按 0.8 元收费．

(1)、写出该单位水费 y（元）与每月用水量 x（吨）之间的函数关系式：（写出自变量取值范围）
①用水量小于等于 3000 吨；
②用水量大于 3000 吨．

(2)、某月该单位用水 3200 吨，水费是元；若用水 2800 吨，水费元．

(3)、若某月该单位缴纳水费 1580 元，则该单位用水多少吨？

查看试题解析
24. 如图，在△ABC中，点O是AC边上的一动点，过点O作直线MN∥BC，MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。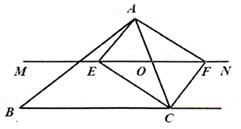

(1)、求证：EO=FO；

(2)、当点O运动到何处时，四边形AECF是矩形？证明你的结论；

(3)、当点O运动到何处时，且△ABC具备什么条件时，四边形AECF是正方形？试说明理由。

查看试题解析

	2014年	2015年	2016年	2017年	2018年
出线成绩(百分制)	79	81	80	81	82

	平均数	方差	中位数
甲	79.6	36.84	78.5
乙	77	147.2	m