2019-2020学年初中数学八年级下学期期末模拟试卷（2）（浙教版）

试卷更新日期：2020-06-24 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围为（）

A、 $x \geq - 2$ B、 $x > 2$ C、 $x \leq 2$ D、 $x \leq - 2$

查看试题解析
2. 如果一个正多边形的中心角等于 $72 °$ ，那么这个多边形的内角和为（）

A、 $360 °$ B、 $540 °$ C、 $720 °$ D、 $900 °$

查看试题解析
3. 为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高(单位：cm)的平均数与方差为：x_甲＝x_丙＝13，x_乙＝x_丁＝15，s_甲²＝s_丁²＝3.6，s_乙²＝s_丙²＝6.3.则麦苗又高又整齐的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 能说明命题“若a>b，则3a>2b”为假命题的反例为（）

A、a=3，b=2 B、a=-2，b=-3 C、a=2，b=3 D、a=-3，b=-2

查看试题解析
5. "桃花流水窅然去，别有天地非人间."桃花园景点2017年三月共接待游客 $a$ 万人，2018年三月比2017年三月旅游人数增加5%，已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%，设2019年三月比2018年三月游客人数增加 $b %$ ，则可列方程为（）

A、 $a (1 + 5 %) (1 + b %) = a (1 + 8 % \times 2)$ B、 $a (1 + 5 %) (1 + b %) = a {(1 + 8 %)}^{2}$ C、 $a (1 + 5 %) (1 + 8 %) = a (1 + b % \times 2)$ D、 $a (1 + 5 %) (1 + 8 %) = 2 a (1 + b %)$

查看试题解析
6. 对于一列数据，如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是（）．

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 关于 $x$ 的一元二次方程 $x^{2} - 2 x + c = 0$ 有两个相等的实数根，则 $c$ 的值是（）

A、 $1$ B、 $- 1$ C、 $\frac{1}{4}$ D、 $- \frac{1}{4}$

查看试题解析
8. 若 $\sqrt{10404}$ =102, $\sqrt{x}$ =10.2，则x等于（　　）

A、1040.4 B、10.404 C、104.04 D、1.0404

查看试题解析
9. 如图，在同一直角坐标系中，函数 $y = k x$ 与 $y = \frac{k}{x} (k \neq 0)$ 的图象大致是（）.

A、①② B、①③ C、②④ D、③④

查看试题解析
10. 如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB，CD交于点E，F，连结BF，交AC于点M，连结DE，BO.若∠BOC=60°，FO=FC，则下列结论：①AE=CF；②BF垂直平分线段OC；③△EOB≌△CMB；④四边形是BFDE菱形.其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 反比例函数 y =(a－3)x^{| a |}^{－ 4}的函数值为4时,自变量 x 的值是.

查看试题解析
12. 如图，平行四边形ABCD的对角线AC与BD相交于点O，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交AO，AB于点M，N；②以点O为圆心，以AM长为半径作弧，交OC于点M'；③以点M'为圆心，以MN长为半径作弧，在∠COB内部交前面的弧于点N'；④过点N'作射线ON'交BC于点E.若AB＝8，则线段OE的长为.

查看试题解析
13. 已知非负数x、y，且xy＝3，那么 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的值为.

查看试题解析
14. 一组数据：23，27，20，18，x，16.它们的平均数是21，则中位数为。

查看试题解析
15. 若菱形的面积为24，一条对角线长为8，则另一条对角线长为，边长为.

查看试题解析
16. 如图，点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点，且HG与EF交于点I，连接HE、FG，若AB=6，BC=5，EF//AD，HG//AB，则HE+FG的最小值是．

查看试题解析

三、解答题

17. 解方程

(1)、 $x^{2} - \sqrt{2} x - \frac{1}{4} = 0$

(2)、 $3 x (x - 1) = 2 (x - 1)$

查看试题解析
18. 如图，在平面直角坐标系中，将矩形ABCD沿直线AE折叠（点E在边DC上），折叠后顶点恰好落在边OC上的点F处，若点D的坐标为（10，8）．

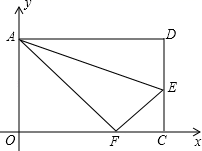(1)、求CE的长；

(2)、写出点E的坐标．

查看试题解析
19. 我校某班级需要选出一名同学去参加温州市“生活中的数学知识”竞赛，现有5名候选人经过了2轮评选。第一轮：由全班50名同学匿名投票，每人选2名同学(不弃权，不重复)，挑选出票数最高的2名同学A与C，已知5名候选人的得票数如图所示。第二轮：根据平时成绩、素养比赛成绩，任课老师打分3项综合分析评选，A、C两名同学的得分情况如表所示。

A

C

平时成绩

90

70

素养比赛成绩

80

80

任课老师打分

70

90

(1)、第一轮5名候选人所得票数的中位数是。

(2)、如果将平时成绩、素养比赛成绩、任课老师打分的得分按5∶3：2的比例确定最后成绩，那么通过排序后最后参加竞赛的是哪位同学？

查看试题解析
20. 阅读下列材料
材料一：对于任意的非零实数x和正实数k，如果满足 $\frac{k x}{3}$ 为整数，则称k是x的一个整商系数，

例如：当 $x = 2 ， k = 3$ 时， $\frac{k x}{3} = 2$ ，则称3是2的一个整商系数；

当 $x = 2 ， k = \frac{3}{2}$ 时， $\frac{k x}{3} = 1$ ，则称 $\frac{3}{2}$ 是2的一个整商系数；

当 $x = - \frac{1}{2} ， k = 6$ 时， $\frac{k x}{3} = - 1$ ，则称6是 $- \frac{1}{2}$ 的一个整商系数；

给论：一个非零实数x有无数个整商系数k，其中最小的一个整商系数记为 $k (x)$ ；

例如： $k (2) = \frac{3}{2} ， k (- \frac{1}{2}) = 6$ ，

材料二：对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两根 $x_{1} ， x_{2}$ ，有如下关系：

$x_{1} + x_{2} = - \frac{b}{a} ， x_{1} \cdot x_{2} = \frac{c}{a}$

请根据材料解决下列问题

(1)、 $k (\frac{7}{2}) =$ $k (- 3) =$

(2)、若关于x的方程： $x^{2} + b x + 2 = 0$ 的两根分别为 $x_{1} ， x_{2}$ ，且满足 $k (x_{1}) + k (x_{2}) = 12$ ，求b的值.

查看试题解析
21. 如图，在矩形ABCD中， $A B = a$ ，点 $E$ ，F分别在BC，CD上，将 $△ A B E$ 沿AE折叠，使点B落在AC上的点 $B^{'}$ 处，又将 $△ C E F$ 沿EF折叠，使点C落在直线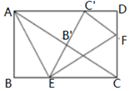 $E B^{'}$ 与AD的交点 $C^{'}$ 处.

(1)、求证：点C在 $∠ E C^{'} D$ 的角平分线上；

(2)、求 $D F$ 的长.

查看试题解析
22. 某游泳池毎次换水前后水的体积基本保持不变，当该游泳池以每小时300立方米的速度放水时，经3小时能将池内的水放完．设放水的速度为x立方米/时，将池内的水放完需y小时．已知该游泳池毎小时的最大放水速度为350立方米

(1)、求y关于x的函数表达式．

(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米（含200立方米和250立方米），求放水时间y的范围．

(3)、该游泳池能否在2.5小时内将池内的水放完？请说明理由．

查看试题解析
23. 已知：正方形ABCD，等腰直角三角形的直角顶点落在正方形的顶点D处，使三角板绕点D旋转.

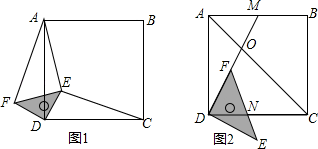(1)、当三角板旋转到图1的位置时，猜想CE与AF的数量关系，并加以证明；

(2)、在（1）的条件下，若DE＝1，AE＝ $\sqrt{7}$ ，CE＝3，求∠AED的度数；

(3)、若BC＝4，点M是边AB的中点，连结DM，DM与AC交于点O，当三角板的一边DF与边DM重合时（如图2），若OF＝ $\frac{\sqrt{5}}{3}$ ，求CN的长.

查看试题解析

	A	C
平时成绩	90	70
素养比赛成绩	80	80
任课老师打分	70	90