2019-2020学年初中数学八年级下学期期末模拟试卷（1）（浙教版）

试卷更新日期：2020-06-24 类型：期末考试

进入出卷网下载

一、单选题

1. 函数 $y = \sqrt{2 x - 3}$ 中自变量 $x$ 的取值范围是（）

A、 $x \geq \frac{3}{2}$ B、 $x \geq - \frac{3}{2}$ C、 $x \leq - \frac{3}{2}$ D、 $x \leq \frac{3}{2}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $3 \sqrt{\frac{1}{3}} = \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $3 + 2 \sqrt{2} = 5 \sqrt{2}$ D、 $- \sqrt{{(- 2)}^{2}} = 2$

查看试题解析
4. 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）

A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°

查看试题解析
5. 如图，点 $Q (m ， n)$ （ $m > 1$ ）是反比例函数 $y = \frac{1}{x}$ 上的动点，过 $Q$ 分别作 $x$ 轴， $y$ 轴的垂线，垂足分别为 $A$ ， $B$ .随着 $m$ 的增大，四边形 $O A Q B$ 的面积（）

A、增大 B、减小 C、不确定 D、不变

查看试题解析
6. 为了更好地培养学生的合作意识，某校采用“团队合作学习”的模式进行学习，学期结束班主任对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：

组别

$1$

$2$

$3$

$4$

$5$

$6$

分值

$94$

$92$

$89$

$88$

$91$

$92$

这组数据的众数和中位数分别是（）

A、 $91, 91.5$ B、 $92, 91.5$ C、 $92, 90$ D、 $90, 92$

查看试题解析
7. 关于x的一元二次方程x²+（m﹣2）x+m+1=0有两个相等的实数根，则m的值是（）

A、0 B、8 C、4±2 D、0或8

查看试题解析
8. 如图，在四边形ABCD中，AC与BD相交于点O ，下列条件不能判定四边形ABCD为平行四边形的是（）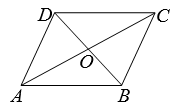

A、AB∥DC ， AB=DC B、AB=DC ， AD=BC C、AB∥DC ， AD=BC D、OA=OC ， OB=OD

查看试题解析
9. 如图，由25个点构成的5×5的正方形点阵中，横、纵方向相邻的两点之间的距离都是1个单位.定义：由点阵中的四个点为顶点的平行四边形叫做阵点平行四边形.图中以A，B为顶点，面积为4的阵点平行四边形的个数为（）

A、6个 B、7个 C、9个 D、11个

查看试题解析
10. 定义新运算： $p \oplus q = {\begin{array}{l} \frac{p}{q} (q > 0) \\ \frac{p}{q} (q < 0) \end{array}$ ，例如： $3 \oplus 5 = \frac{3}{5}$ ， $3 \oplus (- 5) = \frac{3}{5}$ ，则 $y = 2 \oplus x (x \neq 0)$ 的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

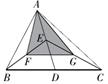
11. 若一个多边形的内角和是外角和的3倍，则该多边形是边形（填该多边形的边数）．

查看试题解析
12. 在本学期的五次数学检测中，甲同学的成绩是： $92, 89, 88, 87, 94$ ，乙同学的成绩是： $78, 88, 92, 94, 98$ ，两名同学成绩比较稳定的是 (填“甲”或“乙”) .

查看试题解析
13. 如图，△ABC的面积是16，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是．

查看试题解析
14. 如图，在正方形ABCD中，AB=6，E为CD上一动点，AE交BD于点F，过F作FH⊥AE，交BC于点H，连结AH、HE，AH与BD交于点G，下列结论：①AF=HE，②∠HAE=45°，③BG²+DF²=GF² ， ④△CEH的周长为12，其中正确的结论有。

查看试题解析
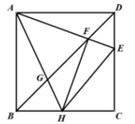15. 菱形两邻角的比为 $1 ： 3$ ，边长为2．则该菱形的面积为．

查看试题解析
16. 如图，在平面直角坐标系中，反比例函数 $y = \frac{3}{x} (x > 0)$ 与正比例函数 $y = k x ， y = \frac{1}{k} x (k > 1)$ 的图像分别交于点A、B，若∠AOB＝45°，则△AOB的面积是.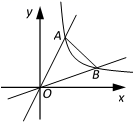

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{40} - 5 \sqrt{\frac{1}{10}} + \sqrt{10}$ ；

(2)、 $\sqrt{48} \div \sqrt{3} - \frac{1}{2} \times \sqrt{12}$ .

查看试题解析
18. 解下列方程

(1)、（3x－1）²＝2（3x－1）

(2)、3x²－2 $\sqrt{3}$ x＋1＝0

查看试题解析
19. 如图，在菱形ABCD中，对角线AC、BD相交于点O，过A作 $A E / / B D$ ，过D作 $D E / / A C ， A E$ 与DE相交于点E.求证：四边形AODE为矩形.

查看试题解析
20. 如图7，已知平行四边形ABCD的周长是32cm，AB︰BC=5︰3，AE⊥BC，垂足为E，AF⊥CD，垂足为F，∠EAF=2∠C.

(1)、求∠C的度数；

(2)、已知DF的长是关于 $x$ 的方程 $x^{2}$ - $a x$ -6=0的一个根，求该方程的另一个根.

查看试题解析

21. 王达和李力是八(2)班运动素质最好的两位同学，为了选出一名同学参加全校的体育运动大寒，班主任针对学校要测试的五个项目，对两位同学进行相应的测试(成绩：分)，结果如下：

姓名	力量	速度	耐力	柔韧	灵敏
王达	60	75	100	90	75
李力	70	90	80	80	80

根据以上测试结果解答下列问题：

(1)、补充完成下表：

姓名	平均成绩(分)	中位数(分)	众数(分)	方差(分²)
王达	80	75	75	190
李力

(2)、任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由；

(3)、若按力量：速度：耐力：柔韧：灵敏=1：2：3：3：1的比例折合成综合分数，推选得分同学参加比赛，请通过计算说明应推选哪位同学去参赛。

查看试题解析

22. 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业．据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数量是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座．

(1)、计划到2020年底，全省5G基站的数量是多少万座？

(2)、按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率；

(3)、求2021年底全省5G基站的数量．

查看试题解析
23. 如图，已知直线y＝x﹣3与双曲线y＝ $\frac{k}{x}$ （k＞0）交于A、B两点，点A的纵坐标为1.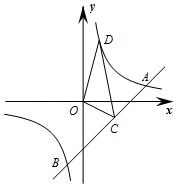

(1)、求点B的坐标；

(2)、直接写出当x在什么范围内时，代数式x²﹣3x的值小于k的值；

(3)、点C（2，m）是直线AB上一点，点D（n，4）是双曲线y＝ $\frac{k}{x}$ 上一点，将△OCD沿射线BA方向平移，得到△O′C′D′.若点O的对应点O′落在双曲线y＝ $\frac{k}{x}$ 上，求点D的对应点D′的坐标.

查看试题解析
24. 如图1和图2，在△ABC中，AB＝13，BC＝14， $\frac{B H}{A B} = \frac{5}{13}$ .

(1)、探究：
如图1，AH⊥BC于点H，则AH＝， AC＝， △ABC的面积 $S_{Δ A B C}$ ＝.

(2)、拓展：如图2，点D在AC上（可与点A、C重合），分别过点A、C作直线BD的垂线，垂足为E、F，设BD＝x，AE＝m，CF＝n，（当点D与A重合时，我们认为 $S_{Δ A B D}$ ＝0）.
用含x、m或n的代数式表示 $S_{Δ A B D}$ 及 $S_{Δ C B D}$ ；

(3)、求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；

(4)、对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围.
发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.

查看试题解析

组别	$1$	$2$	$3$	$4$	$5$	$6$
分值	$94$	$92$	$89$	$88$	$91$	$92$