浙教版数学八年级上册第二章 特殊三角形 单元测试卷
试卷更新日期:2017-09-21 类型:单元试卷
一、单选题
-
1.
如图,在平面直角坐标系中,点P(﹣1,2)关于直线x=1的对称点的坐标为( )
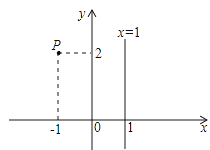 A、(1,2) B、(2,2) C、(3,2) D、(4,2)2. 如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )
A、(1,2) B、(2,2) C、(3,2) D、(4,2)2. 如图,△ABC中,AB=AC,点D在AC边上,若AD=BD=BC,则∠A的度数为( )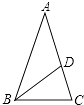 A、70° B、45° C、36° D、30°3. 已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是( )A、7㎝ B、9㎝ C、12㎝或者9㎝ D、12㎝4. 已知一个直角三角形的两边长分别为3和5,则第三边长是( )A、5 B、4 C、 D、4或5. 用反证法证明“在直角三角形中,至少有一个锐角不大于45º”,应先假设这个直角三角形中( )A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º6. 如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5cm,则EF为( )
A、70° B、45° C、36° D、30°3. 已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是( )A、7㎝ B、9㎝ C、12㎝或者9㎝ D、12㎝4. 已知一个直角三角形的两边长分别为3和5,则第三边长是( )A、5 B、4 C、 D、4或5. 用反证法证明“在直角三角形中,至少有一个锐角不大于45º”,应先假设这个直角三角形中( )A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º6. 如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5cm,则EF为( ) A、5 B、10 C、15 D、207. 要判定两个直角三角形全等,下列说法正确的有( )
A、5 B、10 C、15 D、207. 要判定两个直角三角形全等,下列说法正确的有( )①有两条直角边对应相等;
②有两个锐角对应相等;
③有斜边和一条直角边对应相等;
④有一条直角边和一个锐角相等;
⑤有斜边和一个锐角对应相等;
⑥有两条边相等.
A、6个 B、5个 C、4个 D、3个8. 如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )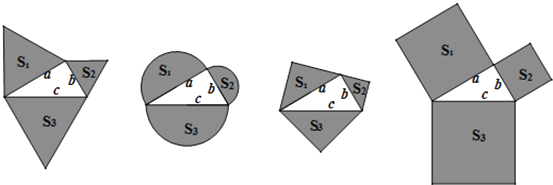 A、1 B、2 C、3 D、49. 如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )
A、1 B、2 C、3 D、49. 如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )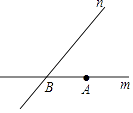 A、1个 B、2个 C、3个 D、4个10. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( )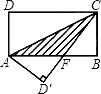 A、8 B、10 C、20 D、32
A、8 B、10 C、20 D、32二、填空题
-
11. 如图,在等腰△ABC的两腰AB、BC上分别取点D和E,使DB=DE,此时恰有∠ADE= ∠ACB,则∠B的度数是 .
 12. 如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,AB=4cm,则∠BCD= , BD= .
12. 如图,△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,AB=4cm,则∠BCD= , BD= .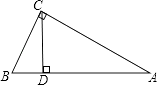 13. 如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=28,则DE= .
13. 如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=28,则DE= .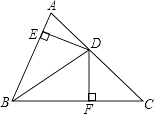 14. 如图,在△ABC中,AC=BC,D是BC边上一点,连接AD,若AB=AD=DC,则∠B= .
14. 如图,在△ABC中,AC=BC,D是BC边上一点,连接AD,若AB=AD=DC,则∠B= .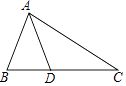 15. 如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是 .
15. 如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是 .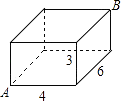
三、解答题
-
16. 已知,a、b、c为△ABC的三边长,b、c满足(b﹣2)2+|c﹣3|=0,且a为方程|a﹣4|=2的解,求△ABC的周长,并判断△ABC的形状.17.
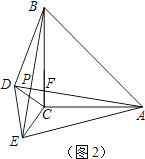
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
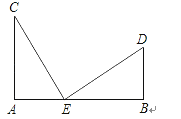 18. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.
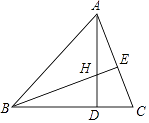
18. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.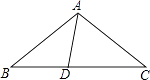 19. 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.
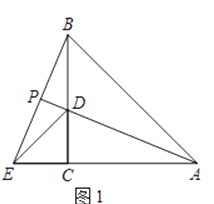
19. 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.试说明△ABC是等腰三角形.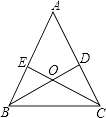 20. 如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.
20. 如图,已知PB⊥AB,PC⊥AC,且PB=PC,D是AP上的一点,求证:BD=CD.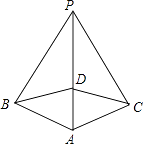
四、综合题
-
21. 如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:
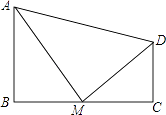 (1)、AM⊥DM;(2)、M为BC的中点.
(1)、AM⊥DM;(2)、M为BC的中点.