河北省唐山市路北区2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期：2017-09-21 类型：期末考试
一、选择题
-
1. 9的平方根是（ ）
A、±3 B、 C、3 D、2. 在平面直角坐标系中，点P（﹣5，0）在（ ）
A、第二象限 B、x轴上 C、第四象限 D、y轴上3. 在﹣2， ， ，3.14， ， ，这6个数中，无理数共有（ ）
A、4个 B、3个 C、2个 D、1个4.如图，AO⊥CO，直线BD经过O点，且∠1=20°，则∠COD的度数为（ ）
A、70° B、110° C、140° D、160°5. 在图中，∠1和∠2是对顶角的是（ ）A、
B、
C、
D、
6. 如果三角形的三个内角的度数比是2：3：4，则它是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、钝角或直角三角形7. 已知方程组 的解满足x+y=2，则k的算术平方根为（ ）A、4 B、﹣2 C、﹣4 D、28. 为了了解2014年我市参加中考的21000名学生的视力情况，从中抽查了1000名学生的视力进行统计分析，下面判断正确的是（ ）
A、21000名学生是总体 B、每名学生是总体的一个个体 C、1000名学生的视力是总体的一个样本 D、上述调查是普查9. 已知三角形的三边分别为2，a，4，那么a的取值范围是（ ）
A、1＜a＜5 B、2＜a＜6 C、3＜a＜7 D、4＜a＜610. 如图，建立适当的直角坐标系后，正方形网格上的点M，N坐标分别为（0，2），（1，1），则点P的坐标为（ ）
A、（﹣1，2） B、（2，﹣1） C、（﹣2，1） D、（1，﹣2）11. 若a＞b，则下列不等式变形正确的是（ ）A、a+5＜b+5 B、＜ C、﹣4a＞﹣4b D、3a﹣2＞3b﹣212.如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=15°，那么∠2的度数是（ ）
A、15° B、25° C、30° D、35°13.如图，△ABC的角平分线BE，CF相交于点O，且∠FOE=121°，则∠A的度数是（ ）
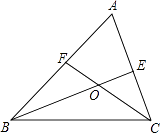A、52° B、62° C、64° D、72°14. 如图a∥b，M、N分别在a、b上，P为两平行线间一点，那么∠1+∠2+∠3=（ ）
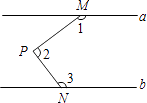A、180° B、270° C、360° D、540°二、填空题
-
15. 在△ABC中，∠A=40°，∠B=∠C，则∠C=°．
16. 一个班级有40人，一次数学考试中，优秀的有18人．在扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是 ．17. 若点（m﹣4，1﹣2m）在第三象限内，则m的取值范围是 ．18.如图，在平面直角坐标系中，A、B的坐标分别为（3，0），（0，2），将线段AB平移至A1B1 ， 则a+b的值为 ．
三、解答题
-
19. 解方程组 ．20. 解不等式组： 并把解集在数轴上表示出来．21. 已知方程组 ，当m为何值时，x＞y？22.
已知，△ABC在直角坐标系中的位置如图所示，现将△ABC先向上平移3个单位，再向左平移2个单位．
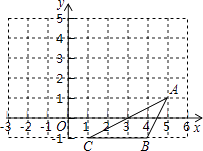(1)、画出两次平移后△ABC的位置（用△ABC表示）；(2)、写出△A1B1C1各顶点的坐标；(3)、求△AA1B1的面积．23.如图，AB∥CD，直线EF与AB，CD分别相交于点E、F，EP平分∠AEF，FP平分∠EFC．
(1)、求证：△EPF是直角三角形；(2)、若∠PEF=30°，直接写出∠PFC的度数．24.网瘾低龄化问题已引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，得到了如图所示的两个不完全统计图．
请根据图中的信息，解决下列问题：
(1)、求条形统计图中a的值；(2)、求扇形统计图中18﹣23岁部分的圆心角；(3)、据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数．25. 某学校准备购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买2个足球和3个篮球共需340元，购买5个足球和2个篮球共需410元．(1)、购买一个足球、一个篮球各需多少元？(2)、根据学校的实际情况，需购买足球和篮球共96个，并且总费用不超过5720元．问最多可以购买多少个篮球？26.已知点A（a，3），点B（b，6），点C（5，c），AC⊥x轴，CB⊥y轴，OB在第二象限的角平分线上：
(1)、写出A，B，C三点坐标；(2)、求△ABC的面积；(3)、若点P为线段OB上动点，当△BCP面积大于12小于16时，求点P横坐标取值范围．