河北省秦皇岛市抚宁县台营学区2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2017-09-21 类型:期末考试
一、精心选一选,慧眼识金!
-
1. 已知a>b,下列不等式中错误的是( )
A、a+1>b+1 B、a﹣2>b﹣2 C、﹣4a<﹣4b D、2a<2b2. 下列命题:①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
A、1个 B、2个 C、3个 D、4个3. 多项式15m3n2+5m2n﹣20m2n3的公因式是( )A、5mn B、5m2n2 C、5m2n D、5mn24. 若△ABC有一个外角是锐角,则△ABC一定是( )A、钝角三角形 B、锐角三角形 C、等边三角形 D、等腰三角形5.如图天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示为( )
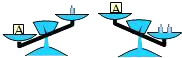 A、
A、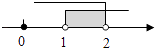 B、
B、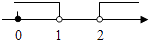 C、
C、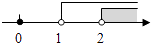 D、
D、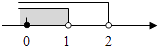 6. 下列运算正确的是( )A、a3•a2=a6 B、2a(3a﹣1)=6a3﹣1 C、(3a2)2=6a4 D、2a+3a=5a7. 下列各式中,能用平方差公因式分解的是( )A、x2+x B、x2+8x+16 C、x2+4 D、x2﹣18. 下列各图中,正确画出AC边上的高的是( )A、
6. 下列运算正确的是( )A、a3•a2=a6 B、2a(3a﹣1)=6a3﹣1 C、(3a2)2=6a4 D、2a+3a=5a7. 下列各式中,能用平方差公因式分解的是( )A、x2+x B、x2+8x+16 C、x2+4 D、x2﹣18. 下列各图中,正确画出AC边上的高的是( )A、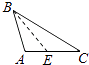 B、
B、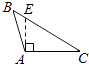 C、
C、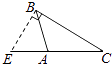 D、
D、 9. 以下列各组线段长为边,能组成三角形的是( )A、1cm,2cm,4cm B、8cm,6cm,4cm C、12cm,5cm,6cm D、2cm,3cm,6cm10.
9. 以下列各组线段长为边,能组成三角形的是( )A、1cm,2cm,4cm B、8cm,6cm,4cm C、12cm,5cm,6cm D、2cm,3cm,6cm10.如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
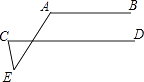 A、60° B、80° C、75° D、70°11.
A、60° B、80° C、75° D、70°11.如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3中能判断直线l1∥l2的有( )
 A、5个 B、4个 C、3个 D、2个12. 已知a﹣b=1,则代数式2a﹣2b﹣3的值是( )A、﹣1 B、1 C、﹣5 D、513. 分解因式2x2﹣4x+2的最终结果是( )A、2x(x﹣2) B、2(x2﹣2x+1) C、2(x﹣1)2 D、(2x﹣2)214.
A、5个 B、4个 C、3个 D、2个12. 已知a﹣b=1,则代数式2a﹣2b﹣3的值是( )A、﹣1 B、1 C、﹣5 D、513. 分解因式2x2﹣4x+2的最终结果是( )A、2x(x﹣2) B、2(x2﹣2x+1) C、2(x﹣1)2 D、(2x﹣2)214.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为2016,则n的值为( )
 A、400 B、401 C、402 D、403
A、400 B、401 C、402 D、403二、填空题
-
15. 把1020000用科学记数法表示为:.16. “a的3倍与4的差不大于1”列出不等式是.17. 如果x2+kx+1是一个完全平方式,那么k的值是 .18. 若am=6,an=2,则am﹣n的值为 .19. 已知关于x的不等式组 有且只有1个整数解,a的取值范围是 .20. 如果a,b,c是整数,且ac=b,那么我们规定一种记号(a,b)=c,例如32=9,那么记作(3,9)=2,根据以上规定,求(﹣2,1)= .
三、解答题
-
21. 解不等式组 ,并把它的解集在数轴上表示出来.22. 先化简,再求值:(x+2)2+(2x+1)(2x﹣1)﹣4x(x+1),其中:x=﹣2.23.
如图,在△BCD中,BC=4,BD=5,
 (1)、求CD的取值范围;(2)、若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.24.
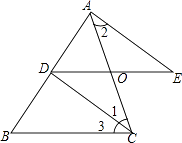
(1)、求CD的取值范围;(2)、若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.24.如图,已知点A,D,B在同一直线上,∠1=∠2,∠3=∠E,若∠DAE=100°,∠E=30°,求∠B的度数.
 25. 列方程组解应用题:
25. 列方程组解应用题:用白铁皮做罐头盒,每张铁皮可制作盒身16个或制盒底40个,一个盒身和两个盒底配成一套罐头盒,现有36张白铁皮用多少张制盒身,多少张制盒底,可以使盒身和盒底正好配套?
26. 先阅读下列材料,再解答下列问题:材料:因式分解:(x+y)2+2(x+y)+1.
解:将“x+y”看成整体,令x+y=A,则
原式=A2+2A+1=(A+1)2
再将“A”还原,得:原式=(x+y+1)2 .
上述解题候总用到的是“整体思想”,整体思想是数学解题中常用的一种思想方法,请你解答下列问题:
(1)、因式分解:1+2(x﹣y)+(x﹣y)2= .(2)、因式分解:(a+b)(a+b﹣4)+4(3)、证明:若n为正整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.