吉林省四平市公主岭市2018-2019学年高二下学期理数期末考试试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 已知复数 ,则复数z的模为( )A、2 B、 C、1 D、02. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 设有一个回归方程为y=2-2.5x,则变量x增加一个单位时( )A、y平均增加2.5个单位 B、y平均增加2个单位 C、y平均减少2.5个单位 D、y平均减少2个单位4. 函数 的图像大致为( )A、
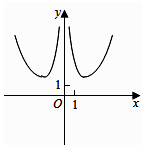 B、
B、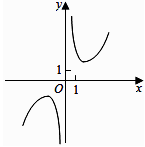 C、
C、 D、
D、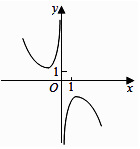 5. 某一批花生种子,如果每1粒发芽的概率为 ,那么播下3粒种子恰有2粒发芽的概率是( )A、 B、 C、 D、6. 在极坐标系中,与 关于极轴对称的点是( )A、 B、 C、 D、7. 若直线 : ( 为参数)经过坐标原点,则直线l的斜率是( )A、-2 B、-1 C、1 D、28. 函数 零点所在的大致区间为( )A、 B、 C、 和 D、9. 设函数 ,则满足 的x的取值范围是( )A、 B、 C、 D、10. 若a>0且 , 且 , 则实数a的取值范围( )A、0<a<1 B、 C、或a>1 D、或11. 已知 为定义在 上的奇函数,当 时, ,则 的值域为( )A、 B、 C、 D、12. 某工厂生产某种产品的产量x(吨)与相应的生产能耗y(吨标准煤)有如下几组样本数据:根据相关检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是( )
5. 某一批花生种子,如果每1粒发芽的概率为 ,那么播下3粒种子恰有2粒发芽的概率是( )A、 B、 C、 D、6. 在极坐标系中,与 关于极轴对称的点是( )A、 B、 C、 D、7. 若直线 : ( 为参数)经过坐标原点,则直线l的斜率是( )A、-2 B、-1 C、1 D、28. 函数 零点所在的大致区间为( )A、 B、 C、 和 D、9. 设函数 ,则满足 的x的取值范围是( )A、 B、 C、 D、10. 若a>0且 , 且 , 则实数a的取值范围( )A、0<a<1 B、 C、或a>1 D、或11. 已知 为定义在 上的奇函数,当 时, ,则 的值域为( )A、 B、 C、 D、12. 某工厂生产某种产品的产量x(吨)与相应的生产能耗y(吨标准煤)有如下几组样本数据:根据相关检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知某商场在一周内某商品日销售量的茎叶图如图所示,那么这一周该商品日销售量的平均数为 .
 14. 若 的二项展开式中的 的系数为9,则 .15. 已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.若P∪Q=Q,求实数a的取值范围 .
14. 若 的二项展开式中的 的系数为9,则 .15. 已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.若P∪Q=Q,求实数a的取值范围 .三、双空题
-
16. 已知直线 与 平行,则 , 与 之间的距离为
四、解答题
-
17. 甲、乙两名篮球运动员,甲投篮的命中率为0.6,乙投篮的命中率为0.7,两人是否投中相互之间没有影响,求:(1)、两人各投一次,只有一人命中的概率;(2)、每人投篮两次,甲投中1球且乙投中2球的概率.18. 在直角坐标平面内,直线l过点P(1,1),且倾斜角α= .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.(1)、求圆C的直角坐标方程;(2)、设直线l与圆C交于A,B两点,求|PA|·|PB|的值.19. 甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为 .记甲击中目标的次数为 ,乙击中目标的次数为 .(1)、求 的分布列;(2)、求 和 的数学期望.20. 已知函数 ( 且 )的图象过定点P,且点P在直线 ( ,且 )上,求 的最小值.21. 从某班6名学生(其中男生4人,女生2人)中任选3人参加学校组织的社会实践活动.设所选3人中女生人数为 ,求 的数学期望.22. 新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
附: ,其中 .
(1)、请完成下面的2×2列联表;选择全理
不选择全理
合计
男生
5
女生
合计
(2)、估计有多大把握认为选择全理与性别有关,并说明理由;(3)、现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.076
3.841
5.024
6.635
7.879
10.828
-