浙江省金衢十二校2020年数学中考模拟联考试卷

试卷更新日期：2020-06-23 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分.每小题只有一个选项是正确的，不选、多选、错选，均不给分）

1. 在－2，－1，0，1这四个数中，最小的数是（）

A、0 B、－1 C、－2 D、1

查看试题解析
2. 下列运算正确的是（）

A、(ab³)²=a²b⁶ B、2a+3b=5ab C、5a²-3a²=2 D、(a+1)²=a²+1

查看试题解析
3. 截止北京时间5月28日，全球新冠肺炎确诊病例逾565万例，将数565万用科学记数法表示为（）

A、565×10⁴ B、56.5×10⁵ C、0.565×10⁷ D、5.65×10⁶

查看试题解析
4. 如图，AB∥CD，∠B＝75°，∠E＝27°，则∠D的度数为（）

A、45° B、48° C、50° D、58°

查看试题解析
5. 不等式组 ${\begin{array}{l} x + 4 > 3 \\ 4 - x > 1 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
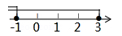6. 在RtΔABC中，∠C=90°，如果sinA= $\frac{1}{3}$ ，那么sinB的值是（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $2 \sqrt{2}$ C、 $\frac{\sqrt{2}}{4}$ D、3

查看试题解析
7. 某几何体的三视图如图所示，则下列说法错误的是（）

A、该几何体是长方体 B、该几何体的高是3 C、该几何体的表面积为18平方单位 D、底面有一边的长是1

查看试题解析
8. 数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a.小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（）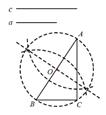

A、勾股定理 B、勾股定理的逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径

查看试题解析
9. 学校有一块长30m，宽20m的矩形空地，计划在这块空地上划出四分之一的区域种花，小阳同学设计方案如图所示，求花带的宽度.设花带的宽度为xm，则可列方程为（）

A、(30－x)(20－x)＝ $\frac{3}{4}$ ×20×30 B、(30－2x)(20－x)＝ $\frac{1}{4}$ ×20×30 C、30x+2×20x＝ $\frac{1}{4}$ ×20×30 D、(30－2x)(20－x)＝ $\frac{3}{4}$ ×20×30

查看试题解析
10. 如图，直线l₁的解析式是y＝ $\frac{\sqrt{3}}{3}$ x，直线l₂的解析式是y＝ $\sqrt{3}$ x，点A₁在l₁上，A₁的横坐标为 $\frac{3}{2}$ ，作A₁B₁⊥l₁交l₂于点B₁ ，点B₂在l₂上，以B₁A₁、B₁B₂为邻边在直线l₁、l₂间作菱形A₁B₁B₂C₁ ，延长B₂C₁交l₁于点A₂ ，点B₃在l₂上，以B₂A₂、B₂B₃为邻边在l₁、l₂间作菱形A₂B₂B₃C₂ ， ………按照此规律继续作下去，则线段A₂₀₂₀B₂₀₂₀长为（）

A、 $2^{2019}$ B、 ${(\frac{3}{2})}^{2019}$ C、 ${(\frac{3}{2})}^{2020}$ D、 ${(\frac{\sqrt{3}}{2})}^{2020}$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 若 $\sqrt{x - 6}$ 在实数范围内有意义，则x的取值范围为.

查看试题解析
12. 如果 $a - b +3 = 0$ ，那么代数式 $2 - 3 a + 3 b$ 的值是.

查看试题解析
13. 如图是一个圆锥形冰淇淋外壳(不计厚度)，已知其母线长为12cm，底面圆半径为3cm，则这个冰淇淋外壳的侧面积等于cm².

查看试题解析
14. 已知二次函数的图象经过点 $P (2 ， 2)$ ，顶点为 $O (0 ， 0)$ 将该图象向右平移，当它再次经过点 $P$ 时，所得抛物线的函数表达式为.

查看试题解析
15. 如图，已知直线 $y = \frac{1}{2} x$ 与反比例函数 $y = \frac{8}{x}$ （x>0）图像交于点A，将直线向右平移4个单位，交反比例函数图象 $y = \frac{8}{x}$ （x>0）于点B，交y轴于点C，连结AB、AC，则△ABC的面积为.

查看试题解析
16. 取一张边长为4的正方形纸折五角星.操作步骤如下：
①按如图1、图2的方法对折两次，将图2展开后得到图3；

②如图4所示折出正方形ABCD对角线的交点O，将纸片折叠，使得点H与点O重合，折痕为EF，再将四边形EFOG折叠，使得EF与FO重合；

③最后再将∠CFO沿着FO折叠，得到图5，沿图中虚线PM剪一刀.展开得图6.

(1)、若图6中∠ABC=36°，则图5中∠MPN=°；

(2)、小王认为此时∠OFC=36°.小黄同学提出了质疑！若已知sin36°= $\frac{\sqrt{5} + 1}{4}$ .请求出sin∠OFC= ，这样就可以知道谁的判断是正确的.

查看试题解析

三、解答题（本题共8小题，共66分）

17. 计算： ${(\frac{1}{2})}^{- 1}$ -2cos30°+ $\sqrt{7}$ +（2-π）⁰

查看试题解析
18. 解方程： $\frac{3 x}{x + 1}$ =2

查看试题解析
19. 定义：在方格纸中，每个小格的顶点叫做格点，以格点为顶点的三角形叫做格点三角形.已知图1，图2中的每一个小方格的边长都为1.

(1)、已知△ABC的三边长为AB= $\sqrt{5}$ ，BC= $\sqrt{10}$ ，AC= $5$ .
①在图1中画一个符合题意的△ABC（C点位置已定）；

②只用无刻度的直尺，在图1中作出△ABC的边BC上的高线；

(2)、在图2中，画出一个与△ABC的面积相等但不全等的三角形.

查看试题解析
20. 某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级（1）班学生即将所穿校服型号情况进行摸底调查，并根据调查结果绘制如图两个不完整的统计图（校服型号以身高作为标准，共分为6种号）.

根据以上信息，解答下列问题：

(1)、该班共有多少名学生？

(2)、在条形统计图中，请把空缺部分补充完整；在扇形统计图中，请计算185型校服所对应的扇形圆心角的大小；

(3)、现在要从2男2女抽取两位学生去试穿校服，问抽到1男1女的概率为多少？

查看试题解析
21. 平行四边形ABCD的对角线相交于点M，ΔABM的外接圆圆心O 恰好落在AD边上，若∠BCD=45°.

(1)、求证：BC为⊙O切线；

(2)、求∠ADB的度数.

查看试题解析
22. 一隧道内设双行公路，隧道的高MN为6米.下图是隧道的截面示意图，并建立如图所示的直角坐标系，它是由一段抛物线和一个矩形CDEF的三条边围成的，矩形的长DE是8米，宽CD是2米.

(1)、求该抛物线的解析式；

(2)、为了保证安全，要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ（居中，两边为人行道）为6米，一辆高3.2米的货运卡车（设为长方形）靠近最右边行驶能否安全？请写出判断过程；

(3)、施工队计划在隧道门口搭建一个矩形“脚手架”ABHG，使H、G两点在抛物线上，A、B两点在地面DE上，设GH长为n米，“脚手架”三根木杆AG、GH、HB的长度之和为L，当n为何值时L最大，最大值为多少？

查看试题解析
23. 城市的许多街道是相互垂直或平行的，因此，往往不能沿直线行走到达目的地，只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy，对两点A（x₁ ， y₁）和B（x₂ ， y₂），用以下方式定义两点间距离：d（A，B）＝|x₁﹣x₂|+|y₁﹣y₂|.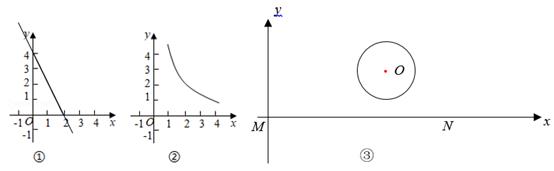

(1)、【数学理解】
①已知点A(－2，1)，则d(O，A)＝.

②函数y＝－2x+4的图象如图①所示，B是图象上一点，d(O，B)＝3，则点B的坐标是.

(2)、函数y＝ $\frac{4}{x}$ (x＞0)的图象如图②所示.求证：该函数图象上不存在点C，使d(O，C)＝3.

(3)、【问题解决】
某市要修建一条通往一圆形景观湖的道路，如图③，道路以M为起点，先沿MN方向到某处，再在该处拐一次直角弯沿直线到湖边某点P处，如图建立坐标系，圆心O(5，3)，半径为 $\sqrt{2}$ ，求修建道路距离d(O，P)的取值范围.

查看试题解析
24. 在矩形ABCD中，AB=3，AD=4，点E是直线AB上的一个动点，连接CE，过点B作BF⊥CE于点G，交射线DA于点F.

(1)、如图1，点E在线段AB上，求证：△ABF∽△BCE；

(2)、如图2，当点E在线段AB上运动到使BE=2AE时，连接DG，求DG的长；

(3)、在点E的运动过程中，是否存在使D、F、G、C四点构成的四边形为轴对称图形，若存在，求出相应AE的长，若不存在，请说明理由.

查看试题解析