浙江省绍兴市柯桥区2020年数学中考模拟试卷(5月)
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题(共10小题).
-
1. 计算:3+(﹣2)结果正确的是( )A、1 B、﹣1 C、5 D、﹣5
-
2. 截止到3月26日0时,全球感染新型冠状病毒肺炎的人数已经突破380000人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将380000用科学记数法表示为( )A、0.38×106 B、3.8×106 C、3.8×105 D、38×104
-
3. 如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
 A、
A、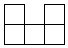 B、
B、 C、
C、 D、
D、
-
4. 某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如表的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、抛一枚硬币,出现正面 B、一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正六面体骰子(六个面上分别标有1,2,3,4,5,6),向上的面点数是5 D、从一个装有2个白球和1个红球的袋子中任取一球,取到红球 -
5. 如图所示,∠α的度数是( )
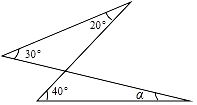 A、10° B、20° C、30° D、40°
A、10° B、20° C、30° D、40° -
6. 已知点A(x1 , a),B(x1+1,b)都在函数y=﹣2x+3的图象上,下列对于a,b的关系判断正确的是( )A、a+b=﹣2 B、a+b=2 C、a﹣b=﹣2 D、a﹣b=2
-
7. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
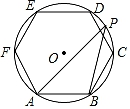 A、15° B、30° C、45° D、60°
A、15° B、30° C、45° D、60° -
8. 在同一平面直角坐标系中,先将抛物线A:y=x2﹣2通过左右平移得到抛物线B,再将抛物线B通过上下平移得到抛物线C:y=x2﹣2x+2,则抛物线B的顶点坐标为( )A、(﹣1,2) B、(1,2) C、(1,﹣2) D、(﹣1,﹣2)
-
9. 如图,矩形ABCD的对角线AC与BD交于点O,AD=1,DC= ,矩形OGHM的边OM经过点D,边OG交CD于点P,将矩形OGHM绕点O逆时针方向旋转α(0°<α<60°),OM′交AD于点F,OG′交CD于点E,设DF=y,EP=x,则y与x的关系为( )
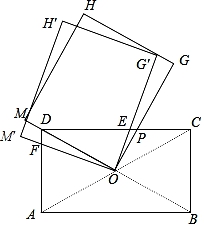 A、y= x B、y= x C、y= x D、y= x
A、y= x B、y= x C、y= x D、y= x -
10. 实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.若乙比甲的水位高2cm时,注水时间m分钟,则m的值为( )
 A、3或5 B、4或6 C、3或 D、5或9
A、3或5 B、4或6 C、3或 D、5或9
二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式:9﹣b2=.
-
12. 计算 的结果是
-
13. 已知a、b都是有理数,观察表中的运算,则m=.
a、b的运算
a+b
a﹣b
(2a+b)3
运算的结果
﹣4
10
m
-
14. 已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=30°,则∠BAC的度数为.
-
15. 如图,直线AB与x的正半轴交于点B,且B(1,0),与y的正半轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= (k≠0)上,将正方形ABCD沿x轴负方向平移2个单位长度,使点D恰好落在双曲线y= (k≠0)上的点D1处,则k=.

-
16. 如图,在等腰三角形ABC中,AC=BC=4,∠A=30°,点D为AC的中点,点E为边AB上一个动点,连接DE,将△ADE沿直线DE折叠,点A落在点F处.当直线EF与直线AC垂直时,则AE的长为.

三、解答题(本题有8小题,第17~20题各8分,第21题10分,第22~23题各12分,第24题14分,共80分)
-
17.(1)、计算:|﹣3|+( +π)0﹣(﹣ )﹣2﹣2cos60°.(2)、解不等式:2(x+3)>4x﹣(x﹣3).
-
18. 某市为了倡导居民节约用水,生活用自来水按阶梯式水价计费.如图是居民每户每月的水(自来水)费y(元)与所用的水(自来水)量x(吨)之间的函数图象.根据如图图象提供的信息,解答下列问题:
 (1)、当一户居民在某月用水为15吨时,求这户居民这个月的水费.(2)、当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨?
(1)、当一户居民在某月用水为15吨时,求这户居民这个月的水费.(2)、当17≤x≤30时,求y与x之间的函数关系式;并计算某户居民上月水费为91元时,这户居民上月用水量多少吨? -
19. 某校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
1
3
5
6
10
15
请根据调查的信息分析:
 (1)、估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.(2)、选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
(1)、估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.(2)、选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果. -
20. 如图①是一个小箱子ABCDE放在桌面MN上的示意图,BC这部分可弯曲,在弯曲时形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,小箱子盖面CD与桌面MN平行,此时CD距离桌面14cm,已知AB的长10cm,CD的长为25.2cm.
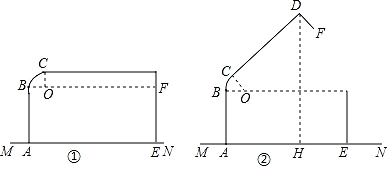 (1)、如图①,求弧BC的长度(结果保留π).(2)、如图②,若小箱子ABCDE打开后弧BC所对的圆心角度数为60°,求小箱子顶端D到桌面MN的距离DH(结果保留一位小数).(参考数据: ≈1.73)
(1)、如图①,求弧BC的长度(结果保留π).(2)、如图②,若小箱子ABCDE打开后弧BC所对的圆心角度数为60°,求小箱子顶端D到桌面MN的距离DH(结果保留一位小数).(参考数据: ≈1.73) -
21. 如图,Rt△ABC中,∠C=90°,AB=4 ,在BC上取一点D,连结AD,作△ACD的外接圆⊙O,交AB于点E.张老师要求添加条件后,编制一道题目,并解答.
 (1)、小明编制题目是:若AD=BD,求证:AE=BE.请你解答.(2)、在小明添加条件的基础上请你再添加一条线段的长度,编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
(1)、小明编制题目是:若AD=BD,求证:AE=BE.请你解答.(2)、在小明添加条件的基础上请你再添加一条线段的长度,编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分) -
22. 某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形,设小正方形的边长m,直角三角形较短边长n,且n=2m﹣4,大正方形的面积为S.
 (1)、求S关于m的函数关系式.(2)、若小正方形边长不大于3,当大正方形面积最大时,求m的值.
(1)、求S关于m的函数关系式.(2)、若小正方形边长不大于3,当大正方形面积最大时,求m的值. -
23. 如图,在△ABC中,G为边AB中点,∠AGC=α.Q为线段BG上一动点(不与点B重合),点P在中线CG上,连接PA,PQ,记BQ=kGP.
 (1)、若α=60°,k=1,
(1)、若α=60°,k=1,①当BQ= BG时,求∠PAG的度数.
②写出线段PA、PQ的数量关系,并说明理由.
(2)、当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由. -
24. 如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ= BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
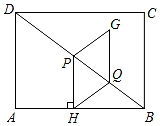 (1)、若m=2时,求此时PH的长.(2)、若点C,G,H在同一直线上时,求此时的m值.(3)、若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.
(1)、若m=2时,求此时PH的长.(2)、若点C,G,H在同一直线上时,求此时的m值.(3)、若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.
