浙江省杭州市萧山区城区六校2020年数学中考模拟试卷(5月)
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 下列各式中,值最小的是( )A、﹣5+3 B、﹣(﹣2)3 C、 D、3÷(﹣ )2. 如图是某几何体的三视图,该几何体是( )
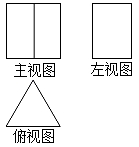 A、长方体 B、三棱锥 C、三棱柱 D、正方体3. 实数a,b,c,d在数轴上的对应点的位置如图所示.若b+d=0,则下列结论正确的是( )
A、长方体 B、三棱锥 C、三棱柱 D、正方体3. 实数a,b,c,d在数轴上的对应点的位置如图所示.若b+d=0,则下列结论正确的是( ) A、b+c>0 B、 >1 C、ad>bc D、|a|>|b|4. 已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )A、x=﹣1,y=2 B、x=﹣1,y=8 C、x=﹣1,y=﹣2 D、x=1,y=85. 长方形的长为10cm、宽为6cm,它的各边都减少xcm,得到的新长方形的周长为ycm,则y与x之间的关系式是( )A、y=32﹣4x(0<x<6) B、y=32﹣4x(0≤x≤6) C、y=(10﹣x)(6﹣x)(0<x<6) D、y=(10﹣x)(6﹣x)(0≤x≤6)6. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变7. 已知平行四边形ABCD,点E是DA延长线上一点,则( )
A、b+c>0 B、 >1 C、ad>bc D、|a|>|b|4. 已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )A、x=﹣1,y=2 B、x=﹣1,y=8 C、x=﹣1,y=﹣2 D、x=1,y=85. 长方形的长为10cm、宽为6cm,它的各边都减少xcm,得到的新长方形的周长为ycm,则y与x之间的关系式是( )A、y=32﹣4x(0<x<6) B、y=32﹣4x(0≤x≤6) C、y=(10﹣x)(6﹣x)(0<x<6) D、y=(10﹣x)(6﹣x)(0≤x≤6)6. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变7. 已知平行四边形ABCD,点E是DA延长线上一点,则( ) A、 = B、 = C、 D、8. 如图,⊙O的半径为2,点A为⊙O上一点,OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
A、 = B、 = C、 D、8. 如图,⊙O的半径为2,点A为⊙O上一点,OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )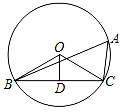 A、 B、 C、1 D、29. 已知函数y1=mx2+n,y2=nx+m(mn≠0),则两个函数在同一坐标系中的图象可能为( )A、
A、 B、 C、1 D、29. 已知函数y1=mx2+n,y2=nx+m(mn≠0),则两个函数在同一坐标系中的图象可能为( )A、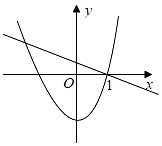 B、
B、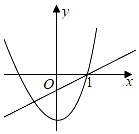 C、
C、 D、
D、 10. 如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )
10. 如图,抛物线y= x2﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是( )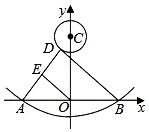 A、 B、 C、3 D、2
A、 B、 C、3 D、2二、填空题:本题有6个小题,每小题4分,共24分.
-
11. 已知 ,则 =.12. 抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(x1 , 0),(x2 , 0),则x1+x2=.13. 如图,在△ABC中,AB=AC,点D,点E分别是BC,AC上一点,且DE⊥AD,若∠BAD=55°,∠B=50°,则∠DEC的度数为.
 14. 如图,以点O为圆心,半径为2的圆与 的图象交于点A,B,若∠AOB=30°,则k的值为.
14. 如图,以点O为圆心,半径为2的圆与 的图象交于点A,B,若∠AOB=30°,则k的值为.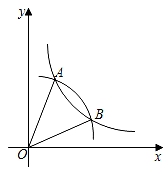 15. 如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为.
15. 如图,△PAB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△PAB与△PCD的面积之差为.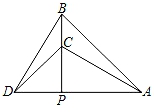 16. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2.
16. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2.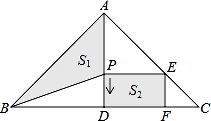
三、解答题:本题有7小题,共66分.
-
17. 已知二次三项式4x2+8x+8,圆圆同学对其进行变形如下:
4x2+8x+8=x2+2x+2=(x+1)2+1,所以圆圆得到结论:当x=﹣1时,这个二次三项式有最小值为1.
圆圆的解答正确吗?如果不正确,写出正确的解答.
18. 如图,在△ABC中,AD平分∠BAC,E是AD上一点,且BE=BD.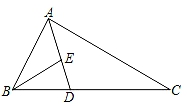 (1)、求证:△ABE∽△ACD;(2)、若BD=1,CD=2,求 的值.19. 如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.
(1)、求证:△ABE∽△ACD;(2)、若BD=1,CD=2,求 的值.19. 如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆.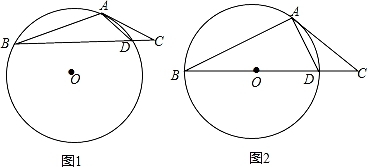 (1)、求证:AC是⊙O的切线;(2)、当BD是⊙O的直径时(如图2),求∠CAD的度数.20. 如图,点A是直线y=2x与反比例函数y= (m为常数)的图象的交点.过点A作x轴的垂线,垂足为B,且OB=2.
(1)、求证:AC是⊙O的切线;(2)、当BD是⊙O的直径时(如图2),求∠CAD的度数.20. 如图,点A是直线y=2x与反比例函数y= (m为常数)的图象的交点.过点A作x轴的垂线,垂足为B,且OB=2.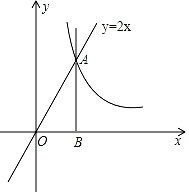 (1)、求点A的坐标及m的值;(2)、已知点P (0,n) (0<n≤8),过点P作平行于x轴的直线,交直线y=2x于点C(x1 , y1),交反比例函数y= (m为常数)的图象于点D(x2 , y2),交垂线AB于点E(x3 , y3),若x2<x3<x1 , 结合函数的图象,直接写出x1+x2+x3的取值范围.21. 某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
(1)、求点A的坐标及m的值;(2)、已知点P (0,n) (0<n≤8),过点P作平行于x轴的直线,交直线y=2x于点C(x1 , y1),交反比例函数y= (m为常数)的图象于点D(x2 , y2),交垂线AB于点E(x3 , y3),若x2<x3<x1 , 结合函数的图象,直接写出x1+x2+x3的取值范围.21. 某学校初二和初三两个年级各有600名同学,为了科普卫生防疫知识,学校组织了一次在线知识竞赛,小宇分别从初二、初三两个年级随机抽取了40名同学的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.a.初二、初三年级学生知识竞赛成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
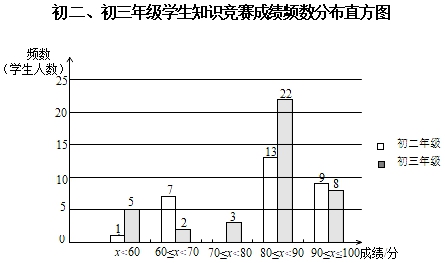
b.初二年级学生知识竞赛成绩在80≤x<90这一组的数据如下:
80 80 81 83 83 84 84 85 86 87 88 89 89
c.初二、初三学生知识竞赛成绩的平均数、中位数、方差如下:
平均数
中位数
方差
初二年级
80.8
m
96.9
初三年级
80.6
86
153.3
根据以上信息,回答下列问题:
(1)、补全上面的知识竞赛成绩频数分布直方图;(2)、写出表中m的值;(3)、A同学看到上述的信息后,说自己的成绩能在本年级排在前40%,B同学看到A同学的成绩后说:“很遗憾,你的成绩在我们年级进不了前50%”.请判断A同学是(填“初二”或“初三”)年级的学生,你判断的理由是.(4)、若成绩在85分及以上为优秀,请估计初二年级竞赛成绩优秀的人数为.