浙江省台州市2020年数学中考押题卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.)
-
1. 下列四个数中,绝对值最大的数是( )A、﹣1 B、0 C、3 D、﹣72. 以下给出的几何体中,主视图是矩形,俯视图是圆的是( )A、
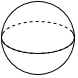 B、
B、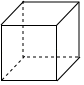 C、
C、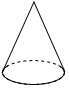 D、
D、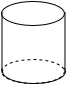 3. 习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近1100万人,将数据1100万用科学记数法表示为( )A、0.11×108 B、1.1×107 C、1.1×108 D、11×1064. 如图,BD∥EF,AE与BD交于点C,∠B=30°,∠A=75°,则∠E的度数为( )
3. 习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近1100万人,将数据1100万用科学记数法表示为( )A、0.11×108 B、1.1×107 C、1.1×108 D、11×1064. 如图,BD∥EF,AE与BD交于点C,∠B=30°,∠A=75°,则∠E的度数为( )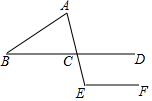 A、135° B、125° C、115° D、105°5. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A、135° B、125° C、115° D、105°5. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )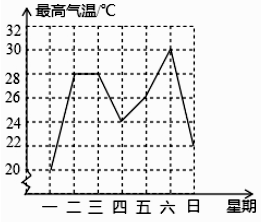 A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问君每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34685个字,设他第一天读x个字,则下面所列方程正确的是( )A、x+2x+4x=34685 B、x+2x+3x=34685 C、x+2x+2x=34685 D、x+ x+ x=346857. 以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P , 若点P的读数为35°,则∠CBD的度数是( )
A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃6. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问君每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34685个字,设他第一天读x个字,则下面所列方程正确的是( )A、x+2x+4x=34685 B、x+2x+3x=34685 C、x+2x+2x=34685 D、x+ x+ x=346857. 以O为中心点的量角器与直角三角板ABC如图所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角板只有一个公共点P , 若点P的读数为35°,则∠CBD的度数是( ) A、55° B、45° C、35° D、258. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A、55° B、45° C、35° D、258. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( ) A、2 B、4 C、 D、9. 抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.
A、2 B、4 C、 D、9. 抛物线y=ax2+bx+c的顶点D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论是( )
 A、③④ B、②④ C、②③ D、①④10. 如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、③④ B、②④ C、②③ D、①④10. 如图,将边长为3的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )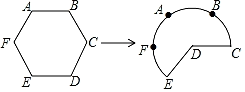 A、S1>S2 B、S1=S2 C、S1<S2 D、S1= S2
A、S1>S2 B、S1=S2 C、S1<S2 D、S1= S2二、填空题(本题有6小题,每小题5分,共30分)
-
11. 分解因式:a3+ab2﹣2a2b=.12. 阅读材料:定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:(4+i)+(6﹣2i)=(4+6)+(1﹣2)i=10﹣i;
(2﹣i)(3+i)=6﹣3i+2i﹣i2=6﹣i﹣(﹣1)=7﹣i;
(4+i)(4﹣i)=16﹣i2=16﹣(﹣1)=17;
(2+i)2=4+4i+i2=4+4i﹣1=3+4i
根据以上信息,完成下面计算:
(1+2i)(2﹣i)+(2﹣i)2=.
13. 不透明袋子中装有红、绿小球各一个,除颜色外无其余差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为.14. 如图,AC是⊙O的直径,弦BD⊥AC于点E,连接BC过点O作OF⊥BC于点F,若BD=12cm,AE=4cm,则OF的长度是cm. 15. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为mm2.
15. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为5mm的小正方形,则每个小长方形的面积为mm2. 16. 如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为.
16. 如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为.
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22,23题每题12分,第24题14分,共80分)
-
17. 计算:( )﹣1+|1﹣ |﹣2sin60°+(π﹣2016)0﹣ .18. 先化简,再求值:(x﹣ )÷ ,其中x=2 .19. 图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC是可伸缩的,其转动点A距离地面BD的高度AE为3.5m.当AC长度为9m,张角∠CAE为112°时,求云梯消防车最高点C距离地面的高度CF.(结果精确到0.1m)
参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40.
 20. 疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.
20. 疫情期间,甲厂欲购买某种无纺布生产口罩,A、B两家无纺布公司各自给出了该种无纺布的销售方案.A公司方案:无纺布的价格y(万元)与其重量x(吨)是如图所示的函数关系;
B公司方案:无纺布不超过30吨时,每吨收费2万元;超过30吨时,超过的部分每吨收费1.9万元.
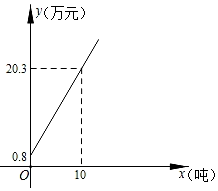 (1)、求如图所示的y与x的函数解析式;(不要求写出定义域)(2)、如果甲厂所需购买的无纺布是40吨,试通过计算说明选择哪家公司费用较少.21. “勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
(1)、求如图所示的y与x的函数解析式;(不要求写出定义域)(2)、如果甲厂所需购买的无纺布是40吨,试通过计算说明选择哪家公司费用较少.21. “勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图: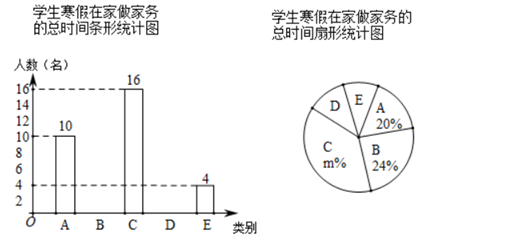
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、请根据以上信息直接在答题卡中补全条形统计图;(3)、扇形统计图中m的值是 , 类别D所对应的扇形圆心角的度数是度;(4)、若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.22. 已知:如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,若∠AEC=∠ODB. (1)、求证:BD是⊙O的切线;(2)、当AB=10,BC=8时,求BD的长.23. 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)、求证:BD是⊙O的切线;(2)、当AB=10,BC=8时,求BD的长.23. 如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.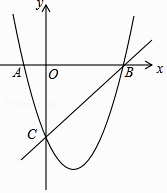 (1)、求这个二次函数的解析式;(2)、是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(1)、求这个二次函数的解析式;(2)、是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)、动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.24. 如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线1与点M同时出发,设运动时间为t秒(t>0).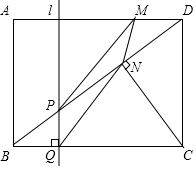 (1)、线段CN=;(2)、连接PM和QN,当四边形MPQN为平行四边形时,求t的值;(3)、在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?
(1)、线段CN=;(2)、连接PM和QN,当四边形MPQN为平行四边形时,求t的值;(3)、在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?