四川省成都市高新区2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、3a2-a2=3 B、a2•a3=a6 C、(a2)3=a6 D、a6÷a2=a32. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线a、b被直线c所截,下列说法错误的是( )
3. 如图,直线a、b被直线c所截,下列说法错误的是( )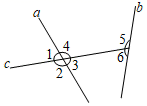 A、∠1与∠5是同位角 B、∠2与∠4是对顶角 C、∠3与∠6是同旁内角 D、∠5与∠6互为余角4. 在圆的周长C=2πR中,常量与变量分别是( )A、2是常量,C、π、R是变量 B、2π是常量,C,R是变量 C、C、2是常量,R是变量 D、2是常量,C、R是变量5. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
A、∠1与∠5是同位角 B、∠2与∠4是对顶角 C、∠3与∠6是同旁内角 D、∠5与∠6互为余角4. 在圆的周长C=2πR中,常量与变量分别是( )A、2是常量,C、π、R是变量 B、2π是常量,C,R是变量 C、C、2是常量,R是变量 D、2是常量,C、R是变量5. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、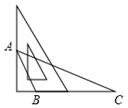 B、
B、 C、
C、 D、
D、 6. 在某次国际乒乓球单打比赛中,两名中国运动员马龙、樊振东进入最后决赛,那么下列事件为必然事件的是( )A、冠军属于中国运动员马龙 B、冠军属于中国运动员樊振东 C、冠军属于中国运动员 D、冠军属于外国运动员7. 下列式子是完全平方式的是( )A、a2+2ab﹣b2 B、a2+2a+1 C、a2+ab+b2 D、a2+2a﹣18. 如图,可以判定AB∥CD的条件是( )
6. 在某次国际乒乓球单打比赛中,两名中国运动员马龙、樊振东进入最后决赛,那么下列事件为必然事件的是( )A、冠军属于中国运动员马龙 B、冠军属于中国运动员樊振东 C、冠军属于中国运动员 D、冠军属于外国运动员7. 下列式子是完全平方式的是( )A、a2+2ab﹣b2 B、a2+2a+1 C、a2+ab+b2 D、a2+2a﹣18. 如图,可以判定AB∥CD的条件是( )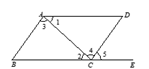 A、∠1=∠2 B、∠3=∠4 C、∠D=∠5 D、∠BAD+∠B=180°9. 如图,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )
A、∠1=∠2 B、∠3=∠4 C、∠D=∠5 D、∠BAD+∠B=180°9. 如图,在△ABC中,∠C=90°,∠B=26°.洋洋按下列步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于EF长的一半为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D,则∠ADC的度数为( )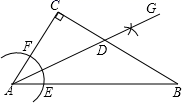 A、50° B、52° C、58° D、64°10. 一列火车从重庆站出发,加速行驶了一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站,乘客上、下车后,火车又加速,一段时间后再次开始匀速行驶,下面哪幅图可以近似地刻画出火车在这段时间内的速度变化情况.( )A、
A、50° B、52° C、58° D、64°10. 一列火车从重庆站出发,加速行驶了一段时间后开始匀速行驶,过了一段时间,火车到达下一个车站,乘客上、下车后,火车又加速,一段时间后再次开始匀速行驶,下面哪幅图可以近似地刻画出火车在这段时间内的速度变化情况.( )A、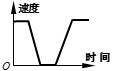 B、
B、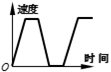 C、
C、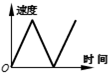 D、
D、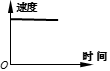
二、填空题
-
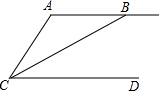
11. 计算:2x2y•(﹣xy)2= .12. 用科学记数法表示:0.007398= .13. 如图,AB∥CD,CB平分∠ACD,若∠BCD=35°,则∠A的度数为.
 14. 已知△ABC是等腰三角形,它的周长为20cm , 一条边长6cm , 那么腰长是 .15. 若am=3,an=2,则a2m﹣n= .16. (2﹣1)(2+1)(22+1)(24+1)…(232+1)的个位数字为 .17. 如图,长方形是由若干个小长方形和小正方形组成,从面积的角度研究这个图形,可以得到一个数学等式,这个数学等式是 . (用图中的字母表示出来)
14. 已知△ABC是等腰三角形,它的周长为20cm , 一条边长6cm , 那么腰长是 .15. 若am=3,an=2,则a2m﹣n= .16. (2﹣1)(2+1)(22+1)(24+1)…(232+1)的个位数字为 .17. 如图,长方形是由若干个小长方形和小正方形组成,从面积的角度研究这个图形,可以得到一个数学等式,这个数学等式是 . (用图中的字母表示出来)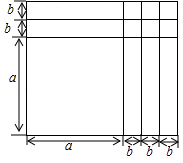 18. 如图,将一张三角形纸片 ABC 的一角折叠,使点 A 落在△ABC 外的 A'处,折痕为 DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么 α,β,γ 三个角的数量关系是 .
18. 如图,将一张三角形纸片 ABC 的一角折叠,使点 A 落在△ABC 外的 A'处,折痕为 DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么 α,β,γ 三个角的数量关系是 .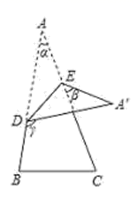 19. 四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为 .
19. 四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为 .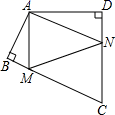
三、解答题
-
20.(1)、计算:(2)、先化简,再求值: ,其中x=2,y=﹣1.21. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
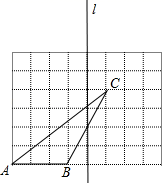 (1)、在图中画出与△ABC关于直线l成轴对称的△A1B1C1;(2)、在直线l上找出一点P,使得|PA﹣PC|的值最大;(保留作图痕迹并标上字母P)(3)、在直线l上找出一点Q,使得QA+QC1的值最小;(保留作图痕迹并标上字母Q)(4)、在正方形网格中存在个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.22. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)、在图中画出与△ABC关于直线l成轴对称的△A1B1C1;(2)、在直线l上找出一点P,使得|PA﹣PC|的值最大;(保留作图痕迹并标上字母P)(3)、在直线l上找出一点Q,使得QA+QC1的值最小;(保留作图痕迹并标上字母Q)(4)、在正方形网格中存在个格点,使得该格点与B、C两点构成以BC为底边的等腰三角形.22. 某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.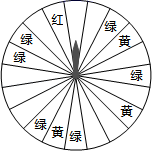 (1)、求转动一次转盘获得购物券的概率;(2)、某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.23. 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
(1)、求转动一次转盘获得购物券的概率;(2)、某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.23. 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?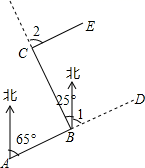 24. 爱动脑筋的小明同学在买一双新的运动鞋时,发现了一个有趣现象:即鞋子的码数y(码)与鞋子的长x(cm)之间存在着某种联系.经过收集数据,得到如表:
24. 爱动脑筋的小明同学在买一双新的运动鞋时,发现了一个有趣现象:即鞋子的码数y(码)与鞋子的长x(cm)之间存在着某种联系.经过收集数据,得到如表:鞋长x(cm)
…
22
23
24
25
26
…
码数y(码)
…
34
36
38
40
42
…
请你替小明解决下列问题:
(1)、当鞋长为28cm时,鞋子的码数是多少?(2)、写出y与x之间的关系式;(3)、已知姚明的鞋子穿52码时,则他穿的鞋长是多长?25. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.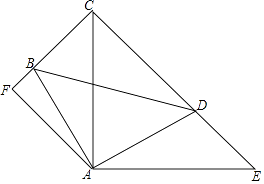 (1)、求证:△ABC≌△ADE;
(1)、求证:△ABC≌△ADE;
(2)、求∠FAE的度数;(3)、求证:CD=2BF+DE.26.(1)、若m2+m﹣1=0,求代数式m3+2m2+2019的值(2)、多项式x3+kx+6能被x+2整除,求常数k的值.27. 五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.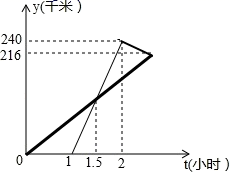 (1)、高铁的平均速度是每小时多少千米?(2)、当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?28. 在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
(1)、高铁的平均速度是每小时多少千米?(2)、当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?28. 在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.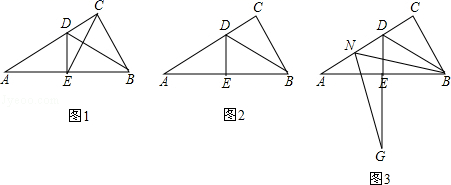 (1)、如图1,连接EC,求证:△EBC是等边三角形;(2)、点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;(3)、如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
(1)、如图1,连接EC,求证:△EBC是等边三角形;(2)、点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;(3)、如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.