山东省淄博市张店区2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 方程组 的解为( )A、 B、 C、 D、2. 下列说法正确的是( )A、两点确定一条直线 B、不相交的两条直线叫做平行线 C、过一点有且只有一条直线与已知直线平行 D、两点间的距离是指连接两点间的线段3. 下列事件中,必然事件是( )A、 一定是正数 B、八边形的外角和等于 C、明天是晴天 D、中秋节晚上能看到月亮4. 如图,△ABC中,∠C=90°,ED垂直平分AB , 若AC=12,EC=5,且△ACE的周长为30,则BE的长为( )
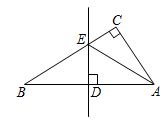 A、5 B、10 C、12 D、135. 不等式组 的解集在数轴上表示为( )A、
A、5 B、10 C、12 D、135. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、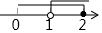 D、
D、 6. 将50个数据分成3组,第一组和第三组的频率之和为0.7,则第二小组的频数是( )A、0.3 B、0.7 C、15 D、357. 若 ,则下列不等式中正确的是( )A、 B、 C、 D、8. 如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O.若AB=AC,∠A=40°,则∠BOE的度数是( )
6. 将50个数据分成3组,第一组和第三组的频率之和为0.7,则第二小组的频数是( )A、0.3 B、0.7 C、15 D、357. 若 ,则下列不等式中正确的是( )A、 B、 C、 D、8. 如图,BD,CE分别是△ABC的高线和角平分线,且相交于点O.若AB=AC,∠A=40°,则∠BOE的度数是( )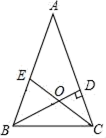 A、60° B、55° C、50° D、40°9. 已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是( )
A、60° B、55° C、50° D、40°9. 已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=60°,则∠2的度数是( )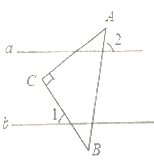 A、70° B、75° C、80° D、85°10. 如图,直线 交坐标轴于A、B两点,则不等式 的解集是( )
A、70° B、75° C、80° D、85°10. 如图,直线 交坐标轴于A、B两点,则不等式 的解集是( )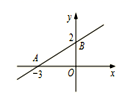 A、 B、 C、 D、11. 如图, ,① ,② ,③ ,④ ,能使 的条件有( )个.
A、 B、 C、 D、11. 如图, ,① ,② ,③ ,④ ,能使 的条件有( )个. A、1 B、2 C、3 D、412. 如图,已知正比例函数y1=ax与一次函数y2= x+b的图象交于点P.下面有四个结论:①a<0; ②b<0; ③当x>0时,y1>0;④当x<﹣2时,y1>y2.其中正确的是( )
A、1 B、2 C、3 D、412. 如图,已知正比例函数y1=ax与一次函数y2= x+b的图象交于点P.下面有四个结论:①a<0; ②b<0; ③当x>0时,y1>0;④当x<﹣2时,y1>y2.其中正确的是( )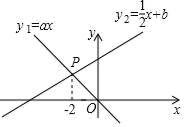 A、①② B、②③ C、①③ D、①④
A、①② B、②③ C、①③ D、①④二、填空题
-
13. 已知方程组 ,那么x﹣y的值为 .14. 如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°;⑤∠6=∠8,其中能判断a∥b的是(填序号)
 15. 小明的生日是6月19日,他用6、1、9这三个数字设置了自己旅行箱三位数字的密码,但是他忘记了数字的顺序,那么他能一次打开旅行箱的概率是.16. 如图,Rt△ABC中,∠C=90°,AD为△ABC的角平分线,与BC相交于点D,若CD=4,AB=15,则△ABD的面积是 .
15. 小明的生日是6月19日,他用6、1、9这三个数字设置了自己旅行箱三位数字的密码,但是他忘记了数字的顺序,那么他能一次打开旅行箱的概率是.16. 如图,Rt△ABC中,∠C=90°,AD为△ABC的角平分线,与BC相交于点D,若CD=4,AB=15,则△ABD的面积是 .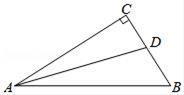 17. 不等式 的正整数解共有个.18. 高速公路某收费站出城方向有编号为 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
17. 不等式 的正整数解共有个.18. 高速公路某收费站出城方向有编号为 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:收费出口编号
通过小客车数量(辆)
260
330
300
360
240
在 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是.
三、解答题
-
19. 解不等式组:20. 填写证明的理由:
已知,如图AB∥CD,EF、CG分别是∠ABC、∠ECD的角平分线.
求证:EF∥CG
证明:∵AB∥CD(已知)
∴∠AEC=∠ECD()
又EF平分∠AEC、CG平分∠ECD(已知)
∴∠1= ∠ , ∠2= ∠(角平分线的定义)
∴∠1=∠2
∴EF∥CG()
 21. 如图,在三角形 中, 是 边的垂直平分线,且分别交 于点 和 , ,求证: 是等边三角形.
21. 如图,在三角形 中, 是 边的垂直平分线,且分别交 于点 和 , ,求证: 是等边三角形. 22. 元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖,指向其余数字不中奖.
22. 元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖,指向其余数字不中奖.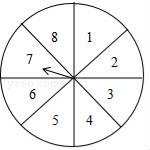 (1)、转动转盘中奖的概率是多少?(2)、元旦期间有1000人参与这项活动,估计获得一等奖的人数是多少?23. 某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
(1)、转动转盘中奖的概率是多少?(2)、元旦期间有1000人参与这项活动,估计获得一等奖的人数是多少?23. 某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:足球
排球
进价(元/个)
80
50
售价(元/个)
95
60
(1)、购进足球和排球各多少个?(2)、全部销售完后商店共获利润多少元?24. 如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,且CD=CE.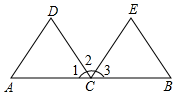 (1)、求证: ;(2)、若 ,求 的度数.25. 如图, 垂直平分线段 ( ),点 是线段 延长线上的一点,且 ,连接 ,过点 作 于点 ,交 的延长线与点 .
(1)、求证: ;(2)、若 ,求 的度数.25. 如图, 垂直平分线段 ( ),点 是线段 延长线上的一点,且 ,连接 ,过点 作 于点 ,交 的延长线与点 .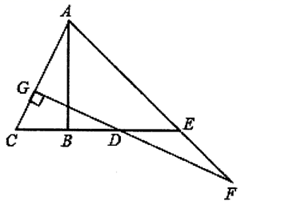 (1)、若 ,则 (用 的代数式表示);(2)、线段 与线段 相等吗?为什么?(3)、若 ,求 的长.26. 某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.(1)、求出乙、丙两种书的每本各多少元?(2)、若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?(3)、在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?(4)、七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?
(1)、若 ,则 (用 的代数式表示);(2)、线段 与线段 相等吗?为什么?(3)、若 ,求 的长.26. 某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读,争当阅读能手”活动,同学们积极响应,涌现出大批的阅读能手.为了激励同学们的阅读热情,养成每天阅读的好习惯,学校对阅读能手进行了奖励表彰,计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品,已知甲、乙、丙三种书的价格比为2:2:3,甲种书每本20元.(1)、求出乙、丙两种书的每本各多少元?(2)、若学校购买甲种书的数量是乙种书的1.5倍,恰好用完计划资金,求甲、乙、丙三种书各买了多少本?(3)、在活动中,同学们表现优秀,学校决定提升奖励档次,增加了245元的购书款,在购买书籍总数不变的情况下,求丙种书最多可以买多少本?(4)、七(1)班阅读氛围浓厚,同伴之间交换书籍共享阅读,已知甲种书籍共270页,小明同学阅读甲种书籍每天21页,阅读5天后,发现同伴比他看得快,为了和同伴及时交换书籍,接下来小明每天多读了a页(20<a<40),结果再用了b天读完,求小明读完整本书共用了多少天?