山东省枣庄市滕州市2018-2019学年七年级下学期数学期末试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是轴对称图形的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列运算正确的是（）

A、 $3 a + 2 a = 5 a^{2}$ B、 ${(2 a)}^{3} = 6 a^{3}$ C、 ${(x + 1)}^{2} = x^{2} + 1$ D、 $(x + 2) (x - 2) = x^{2} - 4$

查看试题解析
3. 若（-2x+a）（x-1）中不含x的一次项，则（）

A、a=1 B、a=-1 C、a=-2 D、a=2

查看试题解析
4. 下列运算结果为 $4 x^{2} - 25 y^{2}$ 的是（）

A、 $(2 x - 5 y) (2 x - 5 y)$ B、 $(- 2 x + 5 y) (2 x + 5 y)$ C、 $(2 x + 5 y) (- 2 x - 5 y)$ D、 $(- 2 x - 5 y) (- 2 x + 5 y)$

查看试题解析
5. 下列事件中必然发生的事件是（）

A、一个图形平移后所得的图形与原来的图形不全等 B、不等式的两边同时乘以一个数，结果仍是不等式 C、200件产品中有5件次品，从中任意抽取6件，至少有一件是正品 D、随意翻到一本书的某页，这页的页码一定是偶数

查看试题解析
6. 从长度分别为2，4，6，8的四条线段中任选三条作边，能构成三角形的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
7. 如图，要使四边形木架（用四根木条钉成）不变形，至少要再钉上的木条的根数为（）

A、1根 B、2根 C、3根 D、4根

查看试题解析
8. 将一副三角板（ $∠ A ＝ 30 ° ， ∠ E ＝ 45 °$ ）按如图所示方式摆放，使得 $B A / / E F$ ，则 $∠ A O F$ 等于（）

A、 $75 °$ B、 $90 °$ C、 $105 °$ D、 $115 °$

查看试题解析
9. 如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于 $\frac{1}{2}$ DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝3，AB＝10，则△ABG的面积是（）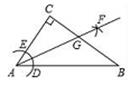

A、3 B、10 C、15 D、30

查看试题解析
10. 对于任意有理数a，b，现用“☆”定义一种运算：a☆b=a²﹣b² ，根据这个定义，代数式（x+y）☆y可以化简为（）

A、xy+y² B、xy﹣y² C、x²+2xy D、x²

查看试题解析
11. 如图，边长为（m+3）的正方形纸片，剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为3，则另一边长是（）

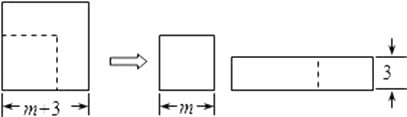A、m+3 B、m+6 C、2m+3 D、2m+6

查看试题解析
12. 将正方形纸片两次对折，并剪出一个菱形小洞后铺平，得到的图形是（）

A、 B、 C、 D、

查看试题解析
13. 如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于CP+EP最小值的是（）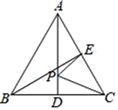

A、AC B、AD C、BE D、BC

查看试题解析
14. 如图，在 $Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ，按如下步骤操作：①以点 $A$ 为圆心，任意长为半径作弧，分别交 $A C$ ， $A B$ 于 $D$ ， $E$ 两点；②以点 $C$ 为圆心， $A D$ 长为半径作弧，交 $A C$ 的延长线于点 $F$ ；③以点 $F$ 为圆心， $D E$ 长为半径作弧，两弧交于点 $G$ ；④作射线 $C G$ ，若 $∠ F C G = 50^{\circ}$ ，则 $∠ B$ 为（）

A、 $40^{\circ}$ B、 $50^{\circ}$ C、 $60^{\circ}$ D、 $70^{\circ}$

查看试题解析
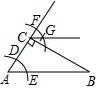15. 甲，乙两人沿相同的路线由 $A$ 地到 $B$ 地匀速前进， $A$ ， $B$ 两地间的路程为 $40 k m$ .他们前进的路程为 $s (k m)$ ，甲出发后的时间为 $t (h)$ ，甲，乙前进的路程与时间的函数图象如图所示.根据图象信息，下列说法错误的是（）

A、甲的速度是 $10 k m / h$ B、乙出发 $\frac{1}{2} h$ 后与甲相遇 C、乙的速度是 $40 k m / h$ D、甲比乙晚到 $B$ 地 $2 h$

查看试题解析

二、填空题

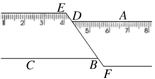
16. 每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为0.0000105m，该数值用科学记数法表示为m.

查看试题解析
17. 如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE＝125°，则∠DBC的度数为．

查看试题解析
18. 若 $x^{2} - 16 x + m^{2}$ 是一个完全平方式，那么 $m$ 的值是.

查看试题解析
19. 在如图所示的正方形纸片上做随机扎针实验，则针头扎在阴影区域内的概率为．

查看试题解析
20. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为．

查看试题解析
21. 如图， $A B = 6 c m$ ， $A C = B D = 4 c m$ . $∠ C A B = ∠ D B A$ ，点 $P$ 在线段 $A B$ 上以 $2 c m / s$ 的速度由点 $A$ 向点 $B$ 运动，同时，点 $Q$ 在线段 $B D$ 上由点 $B$ 向点 $D$ 运动.它们运动的时间为 $t (s)$ .设点 $Q$ 的运动速度为 $x c m / s$ ，若使得 $Δ A C P ≅ Δ B P Q$ 全等，则 $x$ 的值为.

查看试题解析

三、解答题

22. 下列图案由边长相等的黑，白两色正方形按一定规律拼接而成，设第 $x$ 个图案中白色小正方形的个数为 $y$ .

(1)、第2个图案中有个白色的小正方形；第3个图案中有个白色的小正方形； $y$ 与 $x$ 之间的函数表达式为（直接写出结果）.

(2)、是否存在这样的图案，使白色小正方形的个数为2019个?如果存在，请指出是第几个图案；如果不存在，说明理由.

查看试题解析
23. 计算：

(1)、 $- 1^{2020} + {(π - 3)}^{0} + {(\frac{1}{2})}^{- 1}$ ；

(2)、 $9 a \cdot a^{2} \cdot a^{3} + {(- 2 a^{2})}^{3} - a^{8} \div a^{2}$ .

查看试题解析
24. 已知4x=3y，求代数式 ${(x - 2 y)}^{2} - (x - y) (x + y) - 2 y^{2}$ 的值．

查看试题解析
25. 在下列各图中分别补一个小正方形，使其成为不同的轴对称图形．

查看试题解析
26. 如图，点 $B$ 、 $F$ 、 $C$ 、 $E$ 在直线 $l$ 上（ $F$ 、 $C$ 之间不能直接测量），点 $A$ 、 $D$ 在 $l$ 异侧，测得 $A B = D E$ ， $A B$ ∥ $D E$ ， $∠ A = ∠ D$ ．

(1)、求证： $Δ A B C$ ≌ $Δ D E F$ ；

(2)、若 $B E = 10 m$ ， $B F = 3 m$ ，求 $F C$ 的长度．

查看试题解析
27. 如图，△ABC中，AD⊥BC于点D，EF垂直平分AC，交AC于点F，交BC于点E，且BD＝DE，连接AE.

(1)、若∠BAE＝30°，求∠C的度数；

(2)、若△ABC的周长为13cm，AC＝6cm，求DC的长．

查看试题解析
28. 已知 $Δ A B C$ 是直角三角形， $∠ B A C = 90^{\circ}$ ， $A B = A C$ ，直线 $l$ 经过点 $A$ ，分别过点 $B$ 、 $C$ 向直线 $l$ 作垂线，垂足分别为 $D$ 、 $E$ .

(1)、如图1，当点 $B$ ， $C$ 位于直线 $l$ 的同侧时，证明： $Δ A B D ≅ Δ C A E$ .

(2)、如图2，若点 $B$ ， $C$ 在直线 $l$ 的异侧，其它条件不变， $Δ A B D ≅ Δ C A E$ 是否依然成立？请说明理由.

(3)、图形变式：如图3，锐角 $Δ A B C$ 中， $A B = A C$ ，直线 $l$ 经过点 $A$ ，点 $D$ ， $E$ 分别在直线 $l$ 上，点 $B$ ， $C$ 位于 $l$ 的同一侧，如果 $∠ C E A = ∠ A D B = ∠ B A C$ ，请找到图中的全等三角形，并直接写出线段 $E D$ ， $E C$ ， $D B$ 的数量关系.

查看试题解析