浙江省湖州市2020年数学中考押题卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题(每小题3分,共30分)
-
1. ﹣ 的相反数是( )A、﹣ B、 C、﹣ D、2. 在新冠肺炎疫情防控工作中,共产党员充分发挥了先锋模范作用,截止3月4日,全国党员已缴纳特殊党费47.3亿元,用科学记数法表示为( )元.A、4.73×109 B、0.473×1010 C、47.3×108 D、4.73×1083. 下列计算正确的是( )A、a3•a2=a6 B、(﹣3a2b)2=6a4b2 C、﹣a2+2a2=a2 D、(a﹣b)2=a2﹣b24. 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为( )
 A、90° B、45° C、22.5° D、不确定5. 如图,四边形ABCD内接于半径为3的⊙O,CD是直径,若∠ABC=110°,则扇形AOD的面积为( )
A、90° B、45° C、22.5° D、不确定5. 如图,四边形ABCD内接于半径为3的⊙O,CD是直径,若∠ABC=110°,则扇形AOD的面积为( )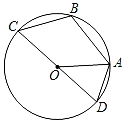 A、 π B、π C、 π D、2π6. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、7. 如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则 的长度为( )
A、 π B、π C、 π D、2π6. 经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是( )A、 B、 C、 D、7. 如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则 的长度为( )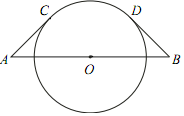 A、π B、2π C、2 π D、4π8. 如图,O为坐标原点,△ABO的两个顶点A(6,0),B(6,6),点D在边AB上,AD=5BD,点C为OA的中点,点P为边OB上的动点,则使四边形PCAD周长最小的点P的坐标为( )
A、π B、2π C、2 π D、4π8. 如图,O为坐标原点,△ABO的两个顶点A(6,0),B(6,6),点D在边AB上,AD=5BD,点C为OA的中点,点P为边OB上的动点,则使四边形PCAD周长最小的点P的坐标为( ) A、(3,3) B、( , ) C、( , ) D、(5,5)9. 如图,正方形MNCB在宽为2的矩形纸片一端,对折正方形MNCB得到折痕AE,再翻折纸片,使AB与AD重合,以下结论错误的是( )
A、(3,3) B、( , ) C、( , ) D、(5,5)9. 如图,正方形MNCB在宽为2的矩形纸片一端,对折正方形MNCB得到折痕AE,再翻折纸片,使AB与AD重合,以下结论错误的是( ) A、AB2=10+2 B、 = C、BC2=CD•EH D、sin∠AHD=10. 二次函数y=ax2+bx+c的部分图象如图所示,有以下结论:①3a﹣b=0;②b2﹣4ac>0;③5a﹣2b+c>0;④4b+3c>0,其中错误结论的个数是( )
A、AB2=10+2 B、 = C、BC2=CD•EH D、sin∠AHD=10. 二次函数y=ax2+bx+c的部分图象如图所示,有以下结论:①3a﹣b=0;②b2﹣4ac>0;③5a﹣2b+c>0;④4b+3c>0,其中错误结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(每小题4分,共24分)
-
11. 分解因式:ab2﹣4a= .
12. 若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .13. 如图,是根据某市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数是. 14. 如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米.
14. 如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米. 15. 如图,在平面直角坐标系中,反比例y= (k>0)的图象和△ABC都在第一象限内,AB=AC= ,BC∥x轴,且BC=4,点A的坐标为(3,5).若将△ABC向下平移m个单位长度,A,C两点同时落在反比例函数图象上,则m的值为.
15. 如图,在平面直角坐标系中,反比例y= (k>0)的图象和△ABC都在第一象限内,AB=AC= ,BC∥x轴,且BC=4,点A的坐标为(3,5).若将△ABC向下平移m个单位长度,A,C两点同时落在反比例函数图象上,则m的值为. 16. 如图,∠EFG=90°,EF=10,OG=17,cos∠FGO= ,则点F的坐标是.
16. 如图,∠EFG=90°,EF=10,OG=17,cos∠FGO= ,则点F的坐标是.
三、解答题(本题有8小题共66分)
-
17. 计算:2•sin30°+|﹣ |+(﹣ )﹣1﹣ .18. 化简:1﹣ ÷ .19. 在画二次函数y=ax2+bx+c(a≠0)的图象时,甲写错了一次项的系数,列表如下
x
……
﹣1
0
1
2
3
……
y甲
……
6
3
2
3
6
……
乙写错了常数项,列表如下:
x
……
﹣1
0
1
2
3
……
y乙
……
﹣2
﹣1
2
7
14
……
通过上述信息,解决以下问题:
(1)、求原二次函数y=ax2+bx+c(a≠0)的表达式;(2)、对于二次函数y=ax2+bx+c(a≠0),当x时,y的值随x的值增大而增大;20. 央视举办的《中国诗词大会》受到广大学生群体广泛关注.某校的诗歌朗诵社团就《中国诗词大会》节目的喜爱程度,在校内对部分学生进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图,请结合图中说给信息解答下列问题: (1)、本次被调查对象共有人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为;(2)、将条形统计图补充完整,并标明数据;(3)、若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.21. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)、本次被调查对象共有人,扇形统计图中被调查者“非常喜欢”等级所对应圆心角的度数为;(2)、将条形统计图补充完整,并标明数据;(3)、若选“不太喜欢”的人中有两名女生,其余是男生,从原“不太喜欢”的人中挑选两名学生了解不太喜欢的原因,请用画树状图或列表法求所选取的这两名学生恰好是一男一女的概率.21. 如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.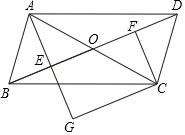 (1)、求证:△ABE≌△CDF;(2)、当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.22. 如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,a米/分的速度骑车向北匀速直行;与此同时,乙从点A出发沿北京路以b米/分的速度步行向东匀速直行.设出发x分钟时,甲、乙两人与点A的距离分别为y1、y2米.已知y1、y2 , 则y1、y2与x之间的函数关系如图②所示.
(1)、求证:△ABE≌△CDF;(2)、当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.22. 如图①,将南北向的中山路与东西向的北京路看成两条直线,十字路口记作点A.甲从中山路上点B出发,a米/分的速度骑车向北匀速直行;与此同时,乙从点A出发沿北京路以b米/分的速度步行向东匀速直行.设出发x分钟时,甲、乙两人与点A的距离分别为y1、y2米.已知y1、y2 , 则y1、y2与x之间的函数关系如图②所示.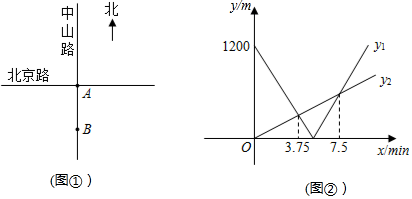 (1)、分别写出y1、y2关于x的函数表达式(用含有a、b的式子表示);(2)、求a、b的值.23. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.
(1)、分别写出y1、y2关于x的函数表达式(用含有a、b的式子表示);(2)、求a、b的值.23. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.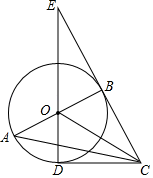 (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=2,DE=4,求圆的半径及AC的长.24. 如图,抛物线y=x2+mx+n与x轴交于A,B两点,与y轴交于点C,若A(﹣1,0),且OC=3OA.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=2,DE=4,求圆的半径及AC的长.24. 如图,抛物线y=x2+mx+n与x轴交于A,B两点,与y轴交于点C,若A(﹣1,0),且OC=3OA.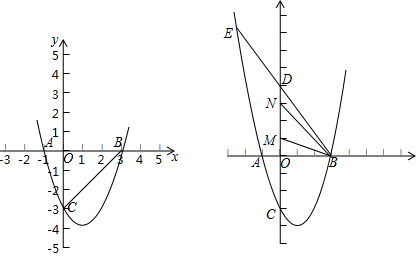 (1)、求抛物线的解析式;(2)、若点M为抛物线上第四象限内一动点,顺次连接AC,CM,MB,是否存在点M,使四边形MBAC的面积为9,若存在,求出点M的坐标,若不存在,请说明理由.(3)、将直线BC沿x轴翻折交y轴于N点,过B点的直线l交y轴、抛物线分别于D、E,且D在N的上方,将A点绕O顺时针旋转90°得M,若∠NBD=∠MBO,试求E的的坐标.
(1)、求抛物线的解析式;(2)、若点M为抛物线上第四象限内一动点,顺次连接AC,CM,MB,是否存在点M,使四边形MBAC的面积为9,若存在,求出点M的坐标,若不存在,请说明理由.(3)、将直线BC沿x轴翻折交y轴于N点,过B点的直线l交y轴、抛物线分别于D、E,且D在N的上方,将A点绕O顺时针旋转90°得M,若∠NBD=∠MBO,试求E的的坐标.