湖北省孝感市孝南区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、选择题

1. $- \frac{1}{64}$ 的立方根是（）

A、－ $\frac{1}{4}$ B、－ $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\pm \frac{1}{4}$

查看试题解析
2. 下列事件适合采用抽样调查的是（）

A、对乘坐飞机的乘客进行安检 B、学校招聘教师，对应聘人员进行面试 C、对“天宫2号”零部件的检查 D、了解全市中小学生每天的午休时间

查看试题解析
3. 下列不等式变形中，一定正确的是（）

A、若ac＞bc，则a＞b B、若a＞b，则am²＞bm² C、若ac²＞bc² ，则a＞b D、若m＞n，则﹣ $\frac{m}{2} > - \frac{n}{2}$

查看试题解析
4. 把不等式组 ${\begin{matrix} 3 x + 1 > - 2 \\ x + 3 \leq 4 \end{matrix}$ 的解集表示在数轴上，下列选项正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列各数中，是无理数的是（）

A、 $\sqrt{16}$ B、3.14 C、 $\frac{3}{11}$ D、 $\sqrt{7}$

查看试题解析
6. 已知方程组 ${\begin{array}{l} x - y = 4 \\ 2 x + y = m \end{array}$ 中的 x，y互为相反数，则m的值为（）

A、2 B、﹣2 C、0 D、4

查看试题解析
7. 如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是（　　）

A、（﹣1，2） B、（﹣9，6） C、（﹣1，6） D、（﹣9，2）

查看试题解析
8. 如图，点F，E分别在线段AB和CD上，下列条件能判定AB∥CD的是（）

A、∠1＝∠2 B、∠1＝∠4 C、∠4＝∠2 D、∠3＝∠4

查看试题解析
9. 如图，面积为64的正方形ABCD被分成4个相同的长方形和1个面积为4的小正方形，则a，b的值分别是（　　）

A、3，5 B、5，3 C、6.5，1.5 D、1.5，6.5

查看试题解析
10. 若不等式组 ${\begin{matrix} 2 x + 9 < 6 x + 1 \\ x - k < 1 \end{matrix}$ 无解，则k的取值范圈为（）

A、k≥1 B、k≤1 C、k＜1 D、k＞1

查看试题解析

二、填空题

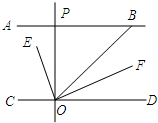
11. 平面直角坐标系中，点 $A$ 在第二象限，到 $x$ 轴的距离是2，到 $y$ 轴的距离是4，则点 $A$ 的坐标为；

查看试题解析
12. 若 $m 、 n$ 为实数,且 $| m + 3 | + \sqrt{n - 3} = 0 ，$ 则 ${(\frac{m}{n})}^{2019}$ 的值为.

查看试题解析
13. 不等式2x+5＞4x﹣1的正整数解是

查看试题解析
14. 某中学为了了解本校3500学生视力情况，在全校范围内随机抽取200名学生进行调查，本次抽样调查的样本容量是.

查看试题解析
15. 《九章算术》中有这样的问题：只闻隔壁人分银，不知多少银和人；每人6两少6两，每人半斤多半斤；试问各位善算者，多少人分多少银？（注：这里的斤是指市斤，1市斤＝10两）设共有x人，y两银子，则可列方程组为.

查看试题解析
16. 如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO＝40°，则下列结论：①∠BOE＝70°；②OF平分∠BOD；③∠POE＝∠BOF；④∠POB＝2∠DOF.其中正确结论有填序号）

查看试题解析

三、解答题

17.

(1)、 ${\begin{matrix} x + 2 y = 0 \\ 3 x + 4 y = 6 \end{matrix}$ ；

(2)、 ${\begin{matrix} \frac{y + 1}{3} = \frac{x + 2}{3} \\ 2 x - 3 y = 1 \end{matrix}$ .

查看试题解析
18. 解不等式（组），并在数轴上表示它的解集

(1)、2（1+x）＜3；

(2)、 ${\begin{array}{l} 2 x + 3 > x + 9 \\ \frac{2 x + 5}{3} > 2 - x \end{array}$ .

查看试题解析

19. 学校为了了解七年学生跳绳情况，从七年级学生中随机抽查了50名学生进行1分钟跳绳测试，并对测试结果统计后绘制了如下不完整统计图表，请根据图表中的信息解答下列问题.

组别	次数	频数（人）	百分比
1	60≤x＜90	5	10%
2	90≤x＜120	5	b
3	120≤x＜150	18	36%
4	150≤x＜180	a	c
5	180≤x＜210	2	4%
合计		50	1

(1)、直接写出a＝， b＝， c＝；

(2)、请补全频数分布直方图；

(3)、若该校七年级共有学生400人，请你估计该校七年级学生跳绳次数在90≤x＜150范围的学生约有多少人？

查看试题解析

20. 在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC三个顶点的位置如图所示，现将△ABC平移，使点A移动到点A'，点B、C的对应点分别是点B'、C'.

(1)、△ABC的面积是；

(2)、画出平移后的△A'B'C'；

(3)、若连接AA'、CC′，这两条线段的关系是.

查看试题解析
21. 已知|2a+b|与 $\sqrt{a + 3 b + 10}$ 互为相反数，

(1)、求a、b的值；

(2)、解关于x的方程：ax²+4b﹣2＝0.

查看试题解析
22. 某商场为做好“家电下乡”的惠民服务，决定从厂家购进甲、乙、丙三种不同型号的电视机108台，其中甲种电视机的台数是丙种的4倍，购进三种电视机的总金额不超过147 000元，已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台，1 500元/台，2 000元/台.

(1)、求该商场至少购买丙种电视机多少台？

(2)、若要求甲种电视机的台数不超过乙种电视机的台数，问有哪些购买方案？

查看试题解析
23. 如图，已知∠BAD+∠ADC＝180°，AE平分∠BAD，CD与AE相交于F，DG交BC的，延长线于G，∠CFE＝∠AEB

(1)、若∠B＝87°，求∠DCG的度数；

(2)、AD与BC是什么位置关系？并说明理由；

(3)、若∠DAB＝α，∠DGC＝β，直接写出α、β满足什么数量关系时，AE∥DG.

查看试题解析
24. 如图，在平面直角坐标系中，OA＝2，OB＝3，现同时将点A，B分别向上平移2个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD.

(1)、求点C、D的坐标及四边形ABDC的面积；

(2)、若点Q在线的CD上移动(不包括C，D两点).QO与线段AB，CD所成的角∠1与∠2如图所示，给出下列两个结论：①∠1+∠2的值不变；② $\frac{∠ 2}{∠ 1}$ 的值不变，其中只有一个结论是正确的，请你找出这个结论，并求出这个值.

(3)、在y轴正半轴上是否存在点P，使得S_△_CDP＝S_△_PBO？如果有，试求出点P的坐标.

查看试题解析