湖北省襄阳市襄州区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、选择题

1. 下列四个实数中最大的是（）

A、 $\sqrt{5}$ B、0 C、1 D、-2

查看试题解析
2. 下列调查中，最适宜采用全面调查方式（普查）的是（）

A、对襄阳市中学生每天课外读书所用时间的调查 B、对全国中学生心理健康现状的调查 C、对七年级（2）班学生 $50$ 米跑步成绩的调查 D、对市面某品牌中性笔笔芯使用寿命的调查

查看试题解析
3. 小手盖住的点的坐标可能为（）

A、 $(5 ， 2)$ B、 $(3 ， - 4)$ C、 $(- 6 ， 3)$ D、 $(- 4 ， - 6)$

查看试题解析
4. 如果a＞b，那么下列各式一定正确的是（）

A、a²＞b² B、 $\frac{a}{2}$ ＜ $\frac{b}{2}$ C、－2a＜－2b D、a－1＜b－1

查看试题解析
5. 将点 $A (2, - 1)$ 向左平移 $3$ 个单位长度，在向上平移 $4$ 个单位长度得到点 $B$ ，则点 $B$ 的坐标是（）

A、 $(5, 3)$ B、 $(5, - 5)$ C、 $(- 1, - 5)$ D、 $(- 1, 3)$

查看试题解析
6. 如图，将直尺与含 $30 °$ 角的直角三角板放在一起，若 $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数是（）

A、 $30 °$ B、 $45 °$ C、 $55 °$ D、 $65 °$

查看试题解析
7. 把不等式组 ${\begin{matrix} x > - 1 \\ x + 2 \leq 3 \end{matrix}$ 的解集表示在数轴上，下列选项正确的是（）

A、 B、 C、 D、

查看试题解析
8. 某班级的一次数学考试成绩统计图如图，则下列说法错误的是（）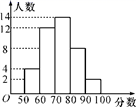

A、得分在70～80分的人数最多 B、该班的总人数为40 C、人数最少的得分段的频数为2 D、得分及格(≥60分)的有12人

查看试题解析
9. 如图，四边形ABCD中，点E在AB延长线上，则下列条件中不能判断AB∥CD的是（）

A、∠3=∠4 B、∠1=∠2 C、∠5=∠C D、∠1+∠3+∠A=180°

查看试题解析
10. 《九章算术》中记载：“今有善田一亩，价三百，恶田七亩，价五百.今并买一顷价钱一万.问善、恶田各几何？”其大意是：今有好田1亩，价值300钱；坏田7亩，价值500钱.今共买好，坏田1顷(1顷＝100亩)，价钱10000钱.问好、坏田各买了多少亩？设好田买了x亩，坏田买了y亩，根意可列方程组为（） ”

A、 ${\begin{array}{l} x + y = 300 \\ 100 x + \frac{500}{7} y = 10000 \end{array}$ B、 ${\begin{array}{l} x + y = 100 \\ 300 x + \frac{500}{7} y = 10000 \end{array}$ C、 ${\begin{array}{l} x + y = 3 = 100 \\ \frac{500}{7} x + 300 y = 10000 \end{array}$ D、 ${\begin{array}{l} x + y = 100 \\ 500 x + \frac{300}{7} y = 10000 \end{array}$

查看试题解析

二、填空题

11. $\sqrt{6} - 3$ 的绝对值是.

查看试题解析
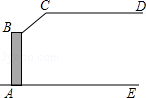
12. 若点（m﹣4，1﹣2m）在第三象限内，则m的取值范围是．

查看试题解析
13. 一大门栏杆的平面示意图如图所示，BA垂直地面AE于点A，CD平行于地面AE，若∠BCD=150°，则∠ABC=度.

查看试题解析
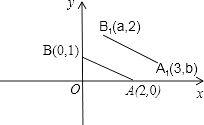
14.
如图，A，B的坐标为（2，0），（0，1）若将线段AB平移至A₁B₁ ，则a+b的值为．

查看试题解析
15. 关于 $x$ 、 $y$ 的二元一次方程组 ${\begin{matrix} 2 x + y = 2 m + 1 \\ x + 2 y = 3 \end{matrix}$ 的解满足不等式 $x - y > 4$ ,则 $m$ 的取值范围是

查看试题解析
16. 已知线段MN平行于x轴，且MN的长度为5，若 $M (2, - 2)$ ，则点N的坐标.

查看试题解析

三、解答题

17. 解方程组： ${\begin{array}{l} 3 x - 2 y = - 1 ① \\ x + 3 y = 7 ② \end{array}$ .

查看试题解析
18. 解不等式组： ${\begin{matrix} 2 (x - 1) < 3 x + 2 \\ \frac{x + 1}{2} > x - 1 \end{matrix}$ ，并将解集在数轴上表示出来.

查看试题解析
19. 甲、乙两名同学在解方程组 ${\begin{matrix} m x + y = 5 \\ 2 x - n y = 13 \end{matrix}$ 时，甲解题时看错了m ，解得 ${\begin{matrix} x = \frac{7}{2} \\ y = - 2 \end{matrix}$ ；乙解题时看错了n ，解得 ${\begin{matrix} x = 3 \\ y = - 7 \end{matrix}$ ．请你以上两种结果，求出原方程组的正确解．

查看试题解析
20. △ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)、分别写出下列各点的坐标： A′；B′；C′；

(2)、若点P（a，b）是△ABC内部一点，则平移后△A′B′C′内的对应点P′的坐标为；

(3)、求△ABC的面积.

查看试题解析
21. 如图所示，已知AF平分∠BAC，DE平分∠BDF，且∠1=∠2.

(1)、能判定DF∥AC吗?为什么?

(2)、能判定DE∥AF吗?为什么?

查看试题解析
22. 某校随机抽取部分学生，对“学习习惯”进行问卷调查．
设计的问题：对自己做错的题目进行整理、分析、改正；

答案选项为：A：很少，B：有时，C：常常，D：总是；

将调查结果的数据进行了整理、绘制成部分统计图如下：

请根据图中信息，解答下列问题：

(1)、该调查的样本容量为， a=%，b=%，“常常”对应扇形的圆心角为；

(2)、请你补全条形统计图；

(3)、若该校有3200名学生，请你估计其中“常常”和“总是”对错题进行整理、分析、改正的学生各有多少名？

查看试题解析
23. 如图，D，E分别是 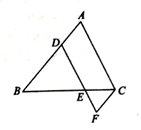$△ A B C$ 边 $A B$ ， $B C$ 上的点， $D E / / A C$ ，点F在 $D E$ 的延长线上，且 $∠ D F C = ∠ A$ .

(1)、试判断 $A B$ 与 $C F$ 的位置关系，并说明理由.

(2)、若 $∠ A C F$ 比 $∠ B D E$ 大 $40 °$ .求 $∠ B D E$ 的度数.

查看试题解析
24. 为了让学生拓展视野、丰富知识，加深与自然和文化的亲近感，增加对集体生活方式和社会公共道德的体验，我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生.为了安全，既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师.现有甲、乙两种大客车，它们的载客量和租金如表所示.

(1)、参加此次研学旅行活动的老师有人；学生有人；租用客车总数为辆；

(2)、设租用 $x$ 辆乙种客车，租车费用为w元，请写出w与x之间的函数关系式；

(3)、在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过 $3100$ 元，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由.

查看试题解析
25. 将一矩形纸片 $O A B C$ 放在直角坐标系中，O为原点，点C在x轴上，点A在Y轴上， $O A = 9 ， O C = 15$ .

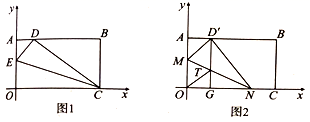(1)、如图1，在 $O A$ 上取一点E，将 $Δ E O C$ 沿 $E C$ 折叠，使O点落在 $A B$ 边上的D点处，求直线 $E C$ 的解析式；

(2)、如图2，在 $O A ， O C$ 边上选取适当的点 $M ， N$ ，将 $Δ M O N$ 沿 $M N$ 折叠，使 $O$ 点落在 $A B$ 边上的点 $D^{'}$ 处，过 $D^{'}$ 作 $D^{'} G ⊥ C O$ 于点 $G$ ，交 $M N$ 于 $T$ 点，连接 $O T$ ，判断四边形 $O T D^{'} M$ 的形状，并说明理由；

(3)、、在（2）的条件下，若点 $T$ 坐标 $(6 ， \frac{5}{2})$ ，点 $P$ 在 $M N$ 直线上，问坐标轴上是否存在点 $Q$ ，使以 $M ， D^{'} ， Q ， P$ 为顶点的四边形是平行四边形，若存在，请直接写出点 $Q$ 坐标；若不存在，请说明理由.

查看试题解析