湖北省咸宁市通城县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-23 类型:期末考试
一、选择题
-
1. 计算 的结果为( )A、6 B、-6 C、18 D、-182. 如图, , 的度数是( )
 A、 B、 C、 D、3. 在平面直角坐标系中,点P(-3,-2019)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式组 的解集在数轴上表示为( )A、
A、 B、 C、 D、3. 在平面直角坐标系中,点P(-3,-2019)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 不等式组 的解集在数轴上表示为( )A、 B、
B、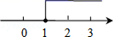 C、
C、 D、
D、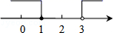 5. 下列调查中,调查方式选择合理的是( )A、为了解襄阳市初中每天锻炼所用时间,选择全面调查 B、为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查 C、为了解神舟飞船设备零件的质量情况,选择抽样调查 D、为了解一批节能灯的使用寿命,选择抽样调查6. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
5. 下列调查中,调查方式选择合理的是( )A、为了解襄阳市初中每天锻炼所用时间,选择全面调查 B、为了解襄阳市电视台《襄阳新闻》栏目的收视率,选择全面调查 C、为了解神舟飞船设备零件的质量情况,选择抽样调查 D、为了解一批节能灯的使用寿命,选择抽样调查6. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( ) A、 B、 C、 D、7. 已知点A(a,3),点B是x轴上一动点,则点A,B之间的距离不可能是( )A、2 B、3 C、4 D、58. 如图是用4个相同的小长方形与一个小正方形密铺而成的大正方形图案.已知大正方形的面积为64,小正方形的面积为9,若用a,b分别表示小长方形的长与宽(其中a>b),则 的值为( )
A、 B、 C、 D、7. 已知点A(a,3),点B是x轴上一动点,则点A,B之间的距离不可能是( )A、2 B、3 C、4 D、58. 如图是用4个相同的小长方形与一个小正方形密铺而成的大正方形图案.已知大正方形的面积为64,小正方形的面积为9,若用a,b分别表示小长方形的长与宽(其中a>b),则 的值为( )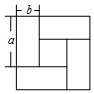 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
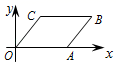
9. 写出一个解为 的二元一次方程组 .10. 点P(3a + 6,3-a)在第四象限内,则a的取值范围为.11. 与﹣π最接近的整数是.12. 已知方程组 , 则x+y的值为 .13. 如图,平行四边形OABC(两组对边分别平行且相等)的顶点A,C的坐标分别为(5,0),(2,3),则顶点B的坐标为.
 14. 佳惠康超市的账目记录显示,某天卖出12支牙刷和9盒牙膏,收入105元;另一天以同样的价格卖出同样的16支牙刷和12盒牙膏,收入应该是元.15. 在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .
14. 佳惠康超市的账目记录显示,某天卖出12支牙刷和9盒牙膏,收入105元;另一天以同样的价格卖出同样的16支牙刷和12盒牙膏,收入应该是元.15. 在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 .
16. 如图,AE∥CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD⊥BC,下列结论:①BC平分∠ABG;②AC∥BG;③与∠DBE互余的角有2个;④若∠A=α,则∠BDF= .其中正确的有.(把你认为正确结论的序号都填上)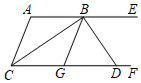
三、解答题
-
17. 解下列方程组:(1)、(2)、18. 解不等式组 并求其整数解.19. 完成下面的证明.
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°.
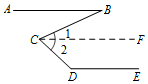
证明:过点C作CF∥AB.
∵CF∥AB(已作),
∴∠1= ▲ .
∵∠2=∠BCD﹣∠1,
∴∠2=∠BCD﹣∠B ▲ .
∵AB∥DE,CF∥AB(已知),
∴CF∥DE▲
∴∠D+∠2=180° ▲
∴∠D+∠BCD﹣∠B=180°▲ .
20. 某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图.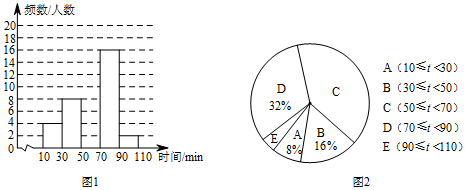
请你根据以上信息解答下列问题:
(1)、本次调查活动采取了调查方式,样本容量是.(2)、图2中C的圆心角度数为 ▲度,补全图1的频数分布直方图.(3)、该校有900名学生,估计该校学生平均每天的课外阅读时间不少于50min的人数.21. 如图,在平面直角坐标系xOy中,已知P(1,2).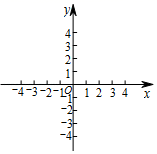 (1)、在平面直角坐标系中描出点P(保留画图痕迹);(2)、如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为.(3)、点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.22. 某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各为多少万元.(2)、甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?23. 我们规定:将任意三个互不相等的数a,b,c按照从小到大的顺序排列后,把处于中间位置的数叫做这三个数的中位数.用符号mid{a,b,c}表示.例如mid{﹣1,2,1}=1.(1)、mid{ ,5,3}=.(2)、当x<﹣2时,求mid{1+x,1﹣x,﹣1}.(3)、若x≠0,且mid{5,5﹣2x,2x+1}=2x+1,求x的取值范围.24. 如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°)
(1)、在平面直角坐标系中描出点P(保留画图痕迹);(2)、如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为.(3)、点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.22. 某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.(1)、求每辆A型车和B型车的售价各为多少万元.(2)、甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?23. 我们规定:将任意三个互不相等的数a,b,c按照从小到大的顺序排列后,把处于中间位置的数叫做这三个数的中位数.用符号mid{a,b,c}表示.例如mid{﹣1,2,1}=1.(1)、mid{ ,5,3}=.(2)、当x<﹣2时,求mid{1+x,1﹣x,﹣1}.(3)、若x≠0,且mid{5,5﹣2x,2x+1}=2x+1,求x的取值范围.24. 如图1,在三角形ABC中,D是BC上一点,且∠CDA=∠CAB.(注:三角形内角和等于180°) (1)、求证:∠CDA=∠DAB+∠DBA;(2)、如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;(3)、将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.
(1)、求证:∠CDA=∠DAB+∠DBA;(2)、如图2,MN是经过点D的一条直线,若直线MN交AC边于点E,且∠CDE=∠CAD.求证:∠AED+∠EAB=180°;(3)、将图2中的直线MN绕点D旋转,使它与射线AB交于点P(点P不与点A,B重合).在图3中画出直线MN,并用等式表示∠CAD,∠BDP,∠BPD这三个角之间的数量关系,不需证明.