湖北省武汉市江岸区（洪山)2018-2019学年七年级下学期数学期末联考试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、选择题

1. 实数 $\sqrt{3}$ 的值在（）

A、0与1之间 B、1与2之间 C、2与3之间 D、3与4之间

查看试题解析
2. 如图，解集在数轴上表示的不等式组为（）

A、 ${\begin{array}{l} x - 2 \geq 0 \\ 3 - x > 0 \end{array}$ B、 ${\begin{array}{l} x + 2 \geq 0 \\ x - 3 > 0 \end{array}$ C、 ${\begin{array}{l} x - 2 \geq 0 \\ 3 + x > 0 \end{array}$ D、 ${\begin{array}{l} 2 - x \geq 0 \\ 3 - x > 0 \end{array}$

查看试题解析
3. 下列调查中，适宜采用全面调查方式的是（）

A、调查春节联欢晚会在武汉市的收视率 B、了解全班同学参加社会实践活动的情况 C、调查某品牌食品的色素含量是否达标 D、了解一批手机电池的使用寿命

查看试题解析
4. 如图，已知 $A B / / C D$ ， $A F$ 与 $C D$ 交于点 $E$ ， $B E ⊥ A F$ ， $∠ B = 50 °$ 则 $∠ D E F$ 得度数是（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
5. 若 $m > n$ ，则下列不等式不成立的是（）

A、 $m - 2 > n - 2$ B、 $3 - m > 3 - n$ C、 $m + 3 a > n + 3 a$ D、 $- \frac{m}{5} < - \frac{n}{5}$

查看试题解析
6. 若 $3 x^{a + 1} y^{2 b}$ 与 $- 4 x^{2} y^{8 - a}$ 是同类项，则（）

A、 $a = 1$ ， $b = \frac{7}{2}$ B、 $a = 1$ ， $b = - \frac{7}{2}$ C、 $a = 1$ ， $b = - 3$ D、 $a = 1$ ， $b = 3$

查看试题解析
7. 《九章算术》中的方程问题：“五只雀、六只燕，共重 $1$ 斤（古代 $1$ 斤= $16$ 两），雀重燕轻，互换其中一只，恰好一样重，问：每只雀、燕的重量各为多少？”设每只雀、燕的重量各为 $x$ 两、 $y$ 两，下列方程组正确的为（）

A、 ${\begin{array}{l} x + y = 16 \\ 4 x + y = x + 5 y \end{array}$ B、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x + y = x + 6 y \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = x + 5 y \end{array}$ D、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 5 x + y = x + 6 y \end{array}$

查看试题解析
8. 如图，已知 $A E$ 平分 $∠ B A C$ ， $B E ⊥ A E$ 于 $E$ ， $E D / / A C$ ，若 $∠ B A E = 36 °$ ，则 $∠ B E D$ 为（）

A、 $136 °$ B、 $126 °$ C、 $124 °$ D、 $114 °$

查看试题解析
9. 关于 $x$ 的不等式组 ${\begin{array}{l} 3 x < 7 b + 3 a \\ 2 x > 6 b - 5 a \end{array}$ 的解集为 $4 < x < 9$ ，则a、b的值是（）

A、 ${\begin{array}{l} a = 2 \\ b = 3 \end{array}$ B、 ${\begin{array}{l} a = - 2 \\ b = 3 \end{array}$ C、 ${\begin{matrix} a = 2 \\ b = - 3 \end{matrix}$ D、 ${\begin{array}{l} a = - 2 \\ b = - 3 \end{array}$

查看试题解析
10. 如图，已知直线 $A B$ 分别交坐标轴于 $A (2 ， 0)$ 、 $B (0 ， - 6)$ 两点，直线上任意一点 $P (x ， y)$ ，设点P到x轴和y轴的距离分别是m和n，则 $m + n$ 的最小值为（）

A、2 B、3 C、5 D、6

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{8}$ = ．

查看试题解析
12. 为了了解某校七年级500名学生的身高情况，从中抽取了100名学生进行测量，这个样本的容量（即样本中个体的数量）是.

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是方程组 ${\begin{array}{l} m x - y = 3 \\ x - n y = 6 \end{array}$ 的解，则 $m - n =$ .

查看试题解析
14. 三角形 $A^{'} B^{'} C^{'}$ 是由三角形 $A B C$ 平移得到的，点 $A (- 1 ， 4)$ 的对应点为 $A^{'} (1 ， - 1)$ ，若点 $C^{'}$ 的坐标为 $(0 ， 0)$ ，则点 $C^{'}$ 的对应点C的坐标为.

查看试题解析
15. 方程组 ${\begin{array}{l} x + y = 2 k \\ x - y = 4 \end{array}$ 的解满足 $x > 1$ ， $y < 1$ ，k的取值范围是：.

查看试题解析
16. 已知 ${\begin{array}{l} x + y + z = 15 \\ - 3 x - y + z = - 25 \end{array}$ ，x、y、z为非负数，且 $N = 5 x + 4 y + z$ ，则N的取值范围是.

查看试题解析

三、解答题

17. 解方程组 ${\begin{matrix} 2 x + y = 1 \\ 2 x - 3 y = - 19 \end{matrix}$

查看试题解析
18. 解不等式组 ${\begin{array}{l} x - 3 < 0 \\ 2 (x + 1) \geq x + 3 \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析

19. 某校举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后随机抽查部分学生的听写结果，以下是根据抽查结果绘制的统计图的一部分.

组别	正确字数x	人数
A	$0 \leq x < 8$	10
B	$8 \leq x < 16$	15
C	$16 \leq x < 24$	25
D	$24 \leq x < 32$	m
E	$32 \leq x < 40$	20

根据以上信息解决下列问题：

(1)、在统计表中，

m =

_▲__，

n =

__▲__，并补全直方图_▲__；

(2)、扇形统计图中“

E

组”所对应的圆心角的度数是度；

(3)、若该校共有964名学生，如果听写正确的个数少于24个定为不合格，请你估计这所学校本次比赛听写不合格的学生人数.

查看试题解析

20. 小明从家里到学校先是走一段平路然后走一段下坡路，假设他始终保持平路每分钟走 $80 m$ ，下坡路每分钟走 $90 m$ ，上坡路每分钟走 $60 m$ ，则他从家里到学校需 $20 m i n$ ，从学校到家里需 $25 m i n$ .
问：从小明家到学校有多远？

查看试题解析
21. 已知，如图，B、C、E三点共线，A、F、E三点共线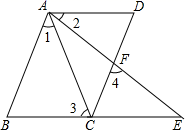， $A B / / C D$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ，求证： $A D / / B E$ .

查看试题解析
22. 某中学计划购买A型和B型课桌凳共200套，经招标，购买一套A型课桌凳比购买一套B型课桌凳少用40元，且购买4套A型和5套B型课桌凳共需1820元.

(1)、求购买一套A型课桌凳和一套B型课桌凳各需多少元？

(2)、学校根据实际情况，要求购买这两种课桌凳的总费用不能超过 $40880$ 元，并且购买 $A$ 型课桌凳的数量不能超过 $B$ 型课桌凳数量的 $\frac{2}{3}$ ，求该校本次购买A型和B型课桌凳共有几种购买方案？怎样的方案使总费用最低？并求出最低消费.

查看试题解析
23. 如图1，已知 $a / / b$ ，点A、B在直线a上，点C、B在直线b上，且 $A D ⊥ B C$ 于E.

(1)、求证： $∠ A B C + ∠ A D C = 90 °$ ；

(2)、如图2， $B F$ 平分 $∠ A B C$ 交 $A D$ 于点F， $D G$ 平分 $∠ A D C$ 交 $B C$ 于点G，求 $∠ A F B + ∠ C G D$ 的度数；

(3)、如图3，P为线段 $A B$ 上一点，I为线段 $B C$ 上一点，连接 $P I$ ，N为 $∠ I P B$ 的角平分线上一点，且 $∠ N C D = \frac{1}{2} ∠ B C N$ ，则 $∠ C I P$ 、 $∠ I P N$ 、 $∠ C N P$ 之间的数量关系是.

查看试题解析
24. 如图，已知 $A (0 ， a)$ ， $B (b ， 0)$ ，且满足 $| a - 4 | + \sqrt{b + 6} = 0$ .

(1)、求A、B两点的坐标；

(2)、点 $C (m ， n)$ 在线段 $A B$ 上，m、n满足 $n - m = 5$ ，点D在y轴负半轴上，连 $C D$ 交 $x$ 轴的负半轴于点 $M$ ，且 $S_{Δ M B C} = S_{Δ M O D}$ ，求点D的坐标；

(3)、平移直线 $A B$ ，交 $x$ 轴正半轴于E，交 $y$ 轴于F，P为直线 $E F$ 上第三象限内的点，过P作 $P G ⊥ x$ 轴于 $G$ ，若 $A_{Δ P A B} = 20$ ，且 $G E = 12$ ，求点P的坐标.

查看试题解析