山东省新泰市(五四制)2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 如图,下列四组条件中,能判断 的是( )
 A、 B、 C、 D、2. 下列事件是必然事件的是( )A、 B、打开电视机,正在播放动画片 C、某种彩票的中奖率为 ,买100张彩票一定中奖 D、13名学生中至少有两个人在同一个月过生日3. 如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为( )
A、 B、 C、 D、2. 下列事件是必然事件的是( )A、 B、打开电视机,正在播放动画片 C、某种彩票的中奖率为 ,买100张彩票一定中奖 D、13名学生中至少有两个人在同一个月过生日3. 如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为( ) A、70° B、80° C、90° D、100°4. 下列说法,正确的是( )A、等腰三角形的高、中线、角平分线互相重合 B、到三角形二个顶点距离相等的点是三边垂直平分线的交点 C、三角形一边上的中线将三角形分成周长相等的两个三角形 D、两边分别相等的两个直角三角形全等5. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、6. 关于 、 的二元一次方程组 的解也是二元一次方程 的解,则k的值是( ).A、 B、 C、 D、7. 不等式组 的解集为 .则 的取值范围为( )A、 B、 C、 D、8. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、70° B、80° C、90° D、100°4. 下列说法,正确的是( )A、等腰三角形的高、中线、角平分线互相重合 B、到三角形二个顶点距离相等的点是三边垂直平分线的交点 C、三角形一边上的中线将三角形分成周长相等的两个三角形 D、两边分别相等的两个直角三角形全等5. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、6. 关于 、 的二元一次方程组 的解也是二元一次方程 的解,则k的值是( ).A、 B、 C、 D、7. 不等式组 的解集为 .则 的取值范围为( )A、 B、 C、 D、8. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )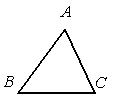 A、
A、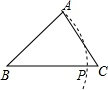 B、
B、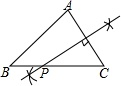 C、
C、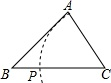 D、
D、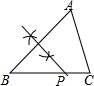 9. 若关于 的不等式组 的整数解共有3个,则 的取值范围是( )A、 B、 C、 D、10. 如图,函数 和 的图象相交于点 ,则关于 的不等式 的解集为( )
9. 若关于 的不等式组 的整数解共有3个,则 的取值范围是( )A、 B、 C、 D、10. 如图,函数 和 的图象相交于点 ,则关于 的不等式 的解集为( ) A、 B、 C、 D、11. 如图,在 中,点 是 边上一点, ,过点 作 交 于 ,若 是等腰三角形,则下列判断中正确的是( )
A、 B、 C、 D、11. 如图,在 中,点 是 边上一点, ,过点 作 交 于 ,若 是等腰三角形,则下列判断中正确的是( ) A、 B、 C、 D、12. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、12. 不等式组 的解集在数轴上表示正确的是( )A、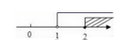 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 正五边形的内角和等于度.14. 某水果店购进苹果与香蕉共 千克进行销售,这两种水果的进价、标价如下表所示,如果店主将这些水果按标价的 折全部售出后,可获利 元,则该水果店购进苹果是千克.
进价(元/千克)
标价(元/千克)
苹果
香蕉
15. 在一个不透明的盒子中装有 个黑球,n个红球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是黑球的概率为 ,则 .16. 如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是 .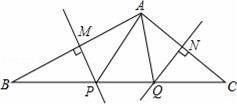 17. 如图,在 中, 是 的垂直平分线,分别交 , 于点 , ,连接 ,若 的周长 , ,则线段 的长度等于cm.
17. 如图,在 中, 是 的垂直平分线,分别交 , 于点 , ,连接 ,若 的周长 , ,则线段 的长度等于cm. 18. 如图,已知 , ,若 平分 , 平分 ,且 ,则 为°.
18. 如图,已知 , ,若 平分 , 平分 ,且 ,则 为°.
三、解答题
-
19. 解方程组20. 解不等式组 ,并写出它的所有非负整数解.21. 元旦期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖,指向其余数字不中奖.
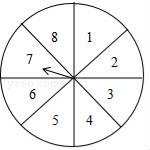 (1)、转动转盘中奖的概率是多少?(2)、元旦期间有1000人参与这项活动,估计获得一等奖的人数是多少?22. 如图, EF∥AD, AD∥BC, CE平分 , .求 的度数.
(1)、转动转盘中奖的概率是多少?(2)、元旦期间有1000人参与这项活动,估计获得一等奖的人数是多少?22. 如图, EF∥AD, AD∥BC, CE平分 , .求 的度数. 23. 如图, 和 都是等边三角形,点 在 的延长线上.
23. 如图, 和 都是等边三角形,点 在 的延长线上. (1)、求证: ;(2)、若 , ,求 的长;(3)、求 的度数.24. 已知:如图, 中, , , 于 ,点 在 的延长线上, ,若 ,求 的长.
(1)、求证: ;(2)、若 , ,求 的长;(3)、求 的度数.24. 已知:如图, 中, , , 于 ,点 在 的延长线上, ,若 ,求 的长. 25. 从我市至枣庄正在修筑的高速公路经过某村,需把本村部分农户搬迁至一个规划区域建房.若这批搬迁农户建房每户占地 ,则规划区域内绿地面积占规划区域总面积的 ;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有 户农户加入建房,若仍以每户占地 计算,则这时绿地面积只占规划区域总面积的 .问:(1)、(列方程组解应用题)最初必须搬迁建房的农户有多少,政府的规划区域总面积是多少平方米?(2)、若要求绿地面积不得少于规划区域总面积的 ,为了符合要求,需要退出部分农户,至少需要退出几户农户?
25. 从我市至枣庄正在修筑的高速公路经过某村,需把本村部分农户搬迁至一个规划区域建房.若这批搬迁农户建房每户占地 ,则规划区域内绿地面积占规划区域总面积的 ;政府又鼓励本村不需要搬迁的农户到规划区域建房,这样又有 户农户加入建房,若仍以每户占地 计算,则这时绿地面积只占规划区域总面积的 .问:(1)、(列方程组解应用题)最初必须搬迁建房的农户有多少,政府的规划区域总面积是多少平方米?(2)、若要求绿地面积不得少于规划区域总面积的 ,为了符合要求,需要退出部分农户,至少需要退出几户农户?