山东省威海市文登区(五四学制)2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 一次函数 和 的图象的交点坐标是( )A、 B、 C、 D、2. 若 ,则下列不等式不一定正确的是( )A、 B、 C、 D、3. 已知 是二元一次不等式组 的一组解,且满足 ,则 的值为( )A、 B、 C、 D、4. 下列说法正确的是( )A、367人中至少有2人生日相同 B、任意掷一枚均匀的骰子,掷出的点数是偶数的概率是 C、天气预报说明天的降水概率为90%,则明天一定会下雨 D、某种彩票中奖的概率是1%,则买100张彩票一定有1张中奖5. 如图,将一副直角三角板按图中所示位置摆放,保持两条斜边互相平行,则∠1的度数是( )
 A、30° B、25° C、20° D、15°6. 如图, 为等边三角形, 是 边上一点,在 上取一点 ,使 ,在 边上取一点 ,使 ,则 的度数为( )
A、30° B、25° C、20° D、15°6. 如图, 为等边三角形, 是 边上一点,在 上取一点 ,使 ,在 边上取一点 ,使 ,则 的度数为( ) A、 B、 C、 D、7. 已知点P(a+1, )关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 已知点P(a+1, )关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
8. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.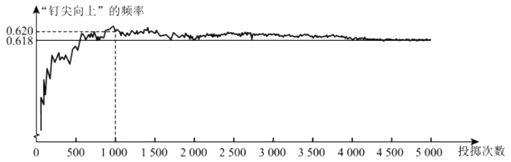
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟此实验,则当投掷次数为1000时,“钉尖向上”的频率一定是0.620.
其中合理的是( )
A、① B、② C、①② D、①③9. 如果不等式组 的解集是 ,那么 的取值范围是( )A、 B、 C、 D、10. 如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )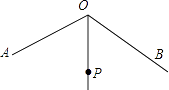 A、1个 B、2个 C、3个 D、3个以上11. 如图,过边长为 的等边 的边 上一点,作 于 为 延长线上一点,当 时,连接 交 于 ,则 的长为( )
A、1个 B、2个 C、3个 D、3个以上11. 如图,过边长为 的等边 的边 上一点,作 于 为 延长线上一点,当 时,连接 交 于 ,则 的长为( )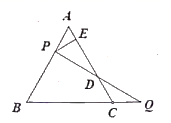 A、 B、 C、 D、12. 某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高()A、40% B、33.4% C、33.3% D、30%
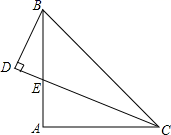
A、 B、 C、 D、12. 某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高()A、40% B、33.4% C、33.3% D、30%二、填空题
-
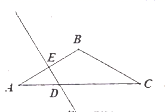
13. 用反证法证明命题“三角形中至少有一个内角大于或等于60°,第一步应假设14. 等腰三角形的一个外角是 ,则这个等腰三角形的底角度数是.15. 从分别标有数-3,-2,-1,0,1,2,3的七张卡片中,随机抽取一张,所抽卡片上数的绝对值小于2的概率是 .16. 已知:如图,在 中, , , 的垂直平分线交 于点 ,交 于点 ,若 ,则 .
 17. 如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b的解集为 .
17. 如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b的解集为 .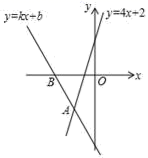
三、解答题
-
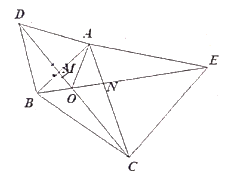
18. 解不等式组:19. 已知:如图,在 中,分别以 为边,在 外作等边 和等边 ,连接 ,分别与 相交于点 ,线段 与线段 交于点 .写出 与 之间的数量关系,并写出证明过程.
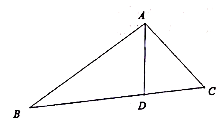
 20. 如图,将等腰直角三角形 的直角顶点置于直线 上,过 两点分别作直线 的垂线,垂足分别为点 ,请你写出图中的一对全等三角形,并写出证明过程.
20. 如图,将等腰直角三角形 的直角顶点置于直线 上,过 两点分别作直线 的垂线,垂足分别为点 ,请你写出图中的一对全等三角形,并写出证明过程.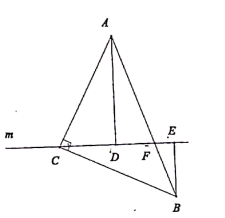 21. 某校随机选取了 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
21. 某校随机选取了 名学生,对他们喜欢的运动项目进行调查,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.项目
学生数
长跑
短跑
跳绳
跳远
200
√
×
√
√
300
×
√
×
√
150
√
√
√
×
200
√
×
√
×
150
√
×
×
×
(1)、估计该校学生同时喜欢短跑和跳绳的概率;(2)、估计该校学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;22. 蔬菜店店主老王,近两天经营的白菜和西兰花的情况如下:(1)、昨天的白菜和西兰花的进价和售价如下表,老王用 元,批发白菜和西兰花共 斤,当天售完后老王一共能赚多少元钱(请列方程解决问题)?白菜
西兰花
进价(元/斤)
售价(元/斤)
(2)、今天因进价不变,老王仍用 元批发白菜和西兰花共 斤.但在运输中白菜损坏了 ,而西兰花没有损坏且仍按昨天的售价销售,要想今天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给白菜定售价?(精确到 元)