山东省青岛市李沧区2018-2019学年七年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 下列手机软件图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项,已知显微镜下某种疟原虫平均长度为0.0000015米,该长度用科学记数法可表示为( )A、 米 B、 米 C、 米 D、 米3. 下列事件中是必然事件是( )A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次,未投中 C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面向上4. 等腰三角形的一个内角为80°,则该三角形其余两个内角的度数分别为( )A、50°,50° B、80°,20° C、80°,50° D、50°,50°或80°,20°5. 下列运算正确的是( )A、 B、 C、 D、2m m =2m6. 如图, ,下列条件中不能使 的是( )
2. 中国药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项,已知显微镜下某种疟原虫平均长度为0.0000015米,该长度用科学记数法可表示为( )A、 米 B、 米 C、 米 D、 米3. 下列事件中是必然事件是( )A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次,未投中 C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面向上4. 等腰三角形的一个内角为80°,则该三角形其余两个内角的度数分别为( )A、50°,50° B、80°,20° C、80°,50° D、50°,50°或80°,20°5. 下列运算正确的是( )A、 B、 C、 D、2m m =2m6. 如图, ,下列条件中不能使 的是( )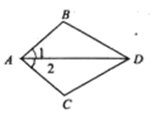 A、 B、 C、 D、7. 把一张对边互相平行的纸条,折成如图所示, 是折痕,若 ,则下列结论正确的有是( )
A、 B、 C、 D、7. 把一张对边互相平行的纸条,折成如图所示, 是折痕,若 ,则下列结论正确的有是( )( 1 ) ;(2) ;(3) ;(4) .
 A、1个 B、2个 C、3个 D、4个8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、1个 B、2个 C、3个 D、4个8. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、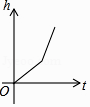 C、
C、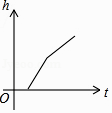 D、
D、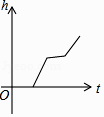
二、填空题
-
9. 有五个面的石块,每个面上分别标记1,2,3,4,5,现随机投掷100次,每个面落在地面上的次数如下表,估计石块标记3的面落在地面上的概率是.
石块的面
1
2
3
4
5
频数
17
28
15
16
24
10. 如图, 平分 , , ,则 . 11. 长方形的周长为 ,其中一边长为 ,面积为 ,则 与 的关系可表示为.12. 一个小区大门栏杆的示意图如图所示, 于A, ,则 .
11. 长方形的周长为 ,其中一边长为 ,面积为 ,则 与 的关系可表示为.12. 一个小区大门栏杆的示意图如图所示, 于A, ,则 . 13. 现有四根长 , , , 的木棒,任取其中的三根,首尾顺次相连后,能组成三角形的概率为.14. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD= BD,点D到边AB的距离为6,则BC的长是 .
13. 现有四根长 , , , 的木棒,任取其中的三根,首尾顺次相连后,能组成三角形的概率为.14. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD= BD,点D到边AB的距离为6,则BC的长是 . 15. 如图,在4×4正方形网格中有3个小方格涂成了灰色.现从剩余的13个白色小方格中选一个也涂成灰色,使整个涂成灰色的图形成轴对称图形,则这样的白色小方格有个.
15. 如图,在4×4正方形网格中有3个小方格涂成了灰色.现从剩余的13个白色小方格中选一个也涂成灰色,使整个涂成灰色的图形成轴对称图形,则这样的白色小方格有个. 16. 1955年,印度数学家卡普耶卡( )研究了对四位自然数的一种变换:任给出四位数 ,用 的四个数字由大到小重新排列成一个四位数 ,再减去它的反序数 (即将 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数 ,然后继续对 重复上述变换,得数 ,…,如此进行下去,卡普耶卡发现,无论 是多大的四位数,只要四个数字不全相同,最多进行 次上述变换,就会出现变换前后相同的四位数 ,这个数称为 变换的核.则四位数9631的 变换的核为.
16. 1955年,印度数学家卡普耶卡( )研究了对四位自然数的一种变换:任给出四位数 ,用 的四个数字由大到小重新排列成一个四位数 ,再减去它的反序数 (即将 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数 ,然后继续对 重复上述变换,得数 ,…,如此进行下去,卡普耶卡发现,无论 是多大的四位数,只要四个数字不全相同,最多进行 次上述变换,就会出现变换前后相同的四位数 ,这个数称为 变换的核.则四位数9631的 变换的核为.三、解答题
-
17. 已知 及其边 上一点 .在 内部求作点 ,使点 到 两边的距离相等,且到点 , 的距离相等.
 18. 计算:(1)、 ;(2)、 ;(3)、先化简再求值 ,其中 , .19. 如图,一个可以自由转动的转盘,分成了四个扇形区域,共有三种不同的颜色,其中红色区域扇形的圆心角为 .小华对小明说:“我们用这个转盘来做一个游戏,指针指向蓝色区域你赢,指针指向红色区域我赢”.你认为这个游戏规则公平吗?请说明理由.
18. 计算:(1)、 ;(2)、 ;(3)、先化简再求值 ,其中 , .19. 如图,一个可以自由转动的转盘,分成了四个扇形区域,共有三种不同的颜色,其中红色区域扇形的圆心角为 .小华对小明说:“我们用这个转盘来做一个游戏,指针指向蓝色区域你赢,指针指向红色区域我赢”.你认为这个游戏规则公平吗?请说明理由.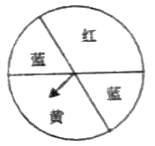 20. 图①,图②都是由一个正方形和一个等腰直角三角形组成的图形.
20. 图①,图②都是由一个正方形和一个等腰直角三角形组成的图形. (1)、用实线把图①分割成六个全等图形;(2)、用实线把图②分割成四个全等图形.21. 如图,点 , 在 上, , , ,试判断 与 有怎样的数量和位置关系,并说明理由.
(1)、用实线把图①分割成六个全等图形;(2)、用实线把图②分割成四个全等图形.21. 如图,点 , 在 上, , , ,试判断 与 有怎样的数量和位置关系,并说明理由.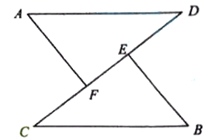 22. 如图,在边长为 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:
22. 如图,在边长为 的正方形四个角上,分别剪去大小相等的等腰直角三角形,当三角形的直角边由小变大时,阴影部分的面积也随之发生变化,它们的变化情况如下:三角形的直角边长/
1
2
3
4
5
6
7
8
9
10
阴影部分的面积/
398
392
382
368
350
302
272
200
 (1)、在这个变化过程中,自变量、因变量各是什么?(2)、请将上述表格补充完整;(3)、当等腰直角三角形的直角边长由 增加到 时,阴影部分的面积是怎样变化的?(4)、设等腰直角三角形的直角边长为 ,图中阴影部分的面积为 ,写出 与 的关系式.23. 问题:将边长为 的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(1)、在这个变化过程中,自变量、因变量各是什么?(2)、请将上述表格补充完整;(3)、当等腰直角三角形的直角边长由 增加到 时,阴影部分的面积是怎样变化的?(4)、设等腰直角三角形的直角边长为 ,图中阴影部分的面积为 ,写出 与 的关系式.23. 问题:将边长为 的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有 个;
边长为2的正三角形一共有1个.

探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有 个;边长为2的正三角形共有 个.
 (1)、探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(1)、探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)
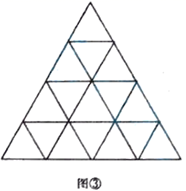 (2)、结论:将边长为 的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(2)、结论:将边长为 的正三角形的三条边分别 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?(仿照上述方法,写出探究过程)
(3)、应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有个和边长为2的正三角形有个.24. 如图,在 中, 为 的中点, , .动点 从点 出发,沿 方向以 的速度向点 运动;同时动点 从点 出发,沿 方向以 的速度向点 运动,运动时间是 秒. (1)、用含 的代数式表示 的长度.(2)、在运动过程中,是否存在某一时刻 ,使点 位于线段 的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.(3)、是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.(4)、是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.
(1)、用含 的代数式表示 的长度.(2)、在运动过程中,是否存在某一时刻 ,使点 位于线段 的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.(3)、是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.(4)、是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.