河南省商丘市梁园区李庄乡2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-06-23 类型:期末考试
一、选择题
-
1. 4的平方根是( )A、 ±2 B、2 C、﹣2 D、162. 点(﹣1,3),( ,5),(0,4),(﹣ ,﹣ )中,在第一象限的是( )A、(﹣1,3) B、( ,5) C、(0,4) D、(﹣ ,﹣ )3. 下列方程是二元一次方程的是( )A、 B、 C、 D、4. 下列说法正确的( )A、调查春节联欢晚会收视率适宜用全面调查 B、要调查一批灯泡的使用寿命适宜用全面调查 C、要调查七年一班学生的年龄适宜全面调查 D、要调查第一小组一次数测评学成绩适宜用抽样调查5. 下列不等式变形中,一定正确的是( )A、若ac>bc,则a>b B、若a>b,则am2>bm2 C、若ac2>bc2 , 则a>b D、若m>n,则﹣6. 解方程组 时,把①代入②,得( )A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、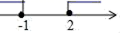 D、
D、 8. 如图,直线a、b被直线c所截,下列说法正确的是( )
8. 如图,直线a、b被直线c所截,下列说法正确的是( )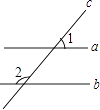 A、当∠1=∠2时,一定有a∥b B、当a∥b时,一定有∠1=∠2 C、当a∥b时,一定有∠1+∠2=90° D、当∠1+∠2=180°时,一定有a∥b9. 平面直角坐标系中,点A(﹣3,2),B(1,4),经过点A的直线L∥x轴,点C直线L上的一个动点,则线段BC的长度最小时点C的坐标为( )A、(﹣1,4) B、(1,0) C、(1,2) D、(4,2)10. 为推进课改,王老师把班级里60名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( )A、4 B、3 C、2 D、1
A、当∠1=∠2时,一定有a∥b B、当a∥b时,一定有∠1=∠2 C、当a∥b时,一定有∠1+∠2=90° D、当∠1+∠2=180°时,一定有a∥b9. 平面直角坐标系中,点A(﹣3,2),B(1,4),经过点A的直线L∥x轴,点C直线L上的一个动点,则线段BC的长度最小时点C的坐标为( )A、(﹣1,4) B、(1,0) C、(1,2) D、(4,2)10. 为推进课改,王老师把班级里60名学生分成若干小组,每小组只能是5人或6人,则有几种分组方案( )A、4 B、3 C、2 D、1二、填空题
-
11. 比较大小: 5(填“ ”或“ ”).12. 如图,直线 、 相交于点 , ,垂足是点 , ,则 的度数为.
 13. 一组数据,最大值与最小值的差为16,取组距为4,则组数为.14. 关于 的方程 的解为非负数,且关于 的不等式组 有解,则符合条件的整数 的值的和为.15. 假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.
13. 一组数据,最大值与最小值的差为16,取组距为4,则组数为.14. 关于 的方程 的解为非负数,且关于 的不等式组 有解,则符合条件的整数 的值的和为.15. 假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过小时车库恰好停满.三、解答题
-
16.(1)、计算(2)、解方程组(3)、解不等式组, 并把解集在数轴上表示出来17. 已知3既是 的算术平方根,又是 的立方根,求 的平方根.18. 如图所示,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,已知∠EGD=40°,求∠BEF的度数
 19. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
19. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:课外阅读时间(单位:小时)
频数(人数)
频率
0<t≤2
2
0.04
2<t≤4
3
0.06
4<t≤6
15
0.30
6<t≤8
a
0.50
t>8
5
b
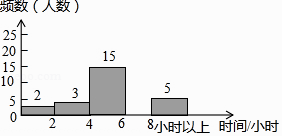
请根据图表信息回答下列问题:
(1)、频数分布表中的a= , b=;(2)、将频数分布直方图补充完整;(3)、学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人?20. 已知关于x、y的方程组 的解x比y的值大1,求方程组的解及k的值.21. 如图,三角形 在直角坐标系中.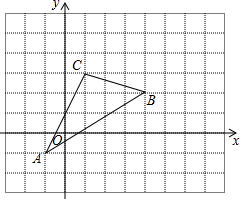 (1)、请直接写出点 、 两点的坐标:(2)、三角形 的面积是;(3)、若把三角形 向上平移1个单位,再向右平移1个单位得三角形 在图中画出三角形 ’ , 这时点 的坐标为.22. 某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.(1)、若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?(2)、按规定,甲种商品的进货不超过50件,甲、乙两种商品共100件的总利润不超过760元,请你通过计算求出该商场所有的进货方案;(3)、在“五一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
(1)、请直接写出点 、 两点的坐标:(2)、三角形 的面积是;(3)、若把三角形 向上平移1个单位,再向右平移1个单位得三角形 在图中画出三角形 ’ , 这时点 的坐标为.22. 某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.(1)、若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求能购进甲、乙两种商品各多少件?(2)、按规定,甲种商品的进货不超过50件,甲、乙两种商品共100件的总利润不超过760元,请你通过计算求出该商场所有的进货方案;(3)、在“五一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:打折前一次性购物总金额
优惠措施
不超过300元
不优惠
超过300元且不超过400元
售价打九折
超过400元
售价打八折
按上述优惠条件,若贝贝第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品各多少件?
23. 如图1, ,点 是直线 、 之间的一点,连接 、 .
 (1)、探究猜想:
(1)、探究猜想:①若 ,则 ▲ .
②若 ,则 ▲ .
③猜想图1中 、 、 的关系,并证明你的结论.
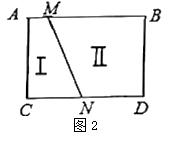
(2)、拓展应用:如图2, ,线段 把 这个封闭区域分为I、II两部分(不含边界),点 是位于这两个区域内的任意一点,请直接写出 、 、 的关系.