山东省莱州市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 如果莱州市2019年6月1日最高气温是 ,最低气温是 ,则当天莱州市气温 的变化范围是( )A、 B、 C、 D、2. 下列说法正确的是( )A、扔100次硬币,都是国徽面向上,是不可能事件 B、小芳在扔图钉游戏中,扔10次,有6次都是钉尖朝下,所以钉尖朝下的可能性大 C、王明同学一直是级部第一名,他能考上重点高中是必然事件 D、投掷一枚均匀的骰子,投出的点数是10,是一个确定事件3. 如图,AC=AD,BC=BD,则有( )
 A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB4. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、
A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB4. 把不等式组 的解集表示在数轴上,下列选项正确的是( )A、 B、
B、 C、
C、 D、
D、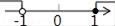 5. 如图,已知直线 , ,且 ,则 等于( )
5. 如图,已知直线 , ,且 ,则 等于( ) A、 B、 C、 D、6. 若 , 则 , , 的大小关系是( )
A、 B、 C、 D、6. 若 , 则 , , 的大小关系是( )
A、 B、 C、 D、7. 关于 、 的二元一次方程组 的解也是二元一次方程 的解,则k的值是( ).A、 B、 C、 D、8. 已知等腰三角形的两边长分别为 和 ,那么这个等腰三角形的周长是( )A、 B、 C、 或 D、不能确定9. “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上),则投掷一次飞镖扎在中间小正方形区域(含边线)的概率是( ) A、 B、 C、 D、10. 如图,点 的坐标是 ,若点 在 轴上,且 是等腰三角形,则点 的坐标不可能是( )
A、 B、 C、 D、10. 如图,点 的坐标是 ,若点 在 轴上,且 是等腰三角形,则点 的坐标不可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 任意抛掷一枚质地均匀的骰子一次,朝上的点数大于4的概率等 .12. 命题“同角的补角相等”的条件是.13. 一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋中随机摸出一球,记下颜色,然后把它放回口袋中.不断重复上述过程.小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有 .
14. 如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3=°. 15. 如图,折叠直角三角形纸片的直角,使点 落在斜边 上的点 处,已知 , ,则 .
15. 如图,折叠直角三角形纸片的直角,使点 落在斜边 上的点 处,已知 , ,则 . 16. 如图, 是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有个等边三角形.
16. 如图, 是等边三角形,过它的三个顶点分别作对边的平行线,则图中共有个等边三角形. 17. 等腰三角形一腰上的高与另一腰的夹角为 ,腰长为2,则其底边上的高为.18. 若不等式组 的解集是-1<x<1,则(a+b)2019= .19. 已知关于x的不等式组 只有四个整数解,则实数a的取值范是 .20. 在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于 .
17. 等腰三角形一腰上的高与另一腰的夹角为 ,腰长为2,则其底边上的高为.18. 若不等式组 的解集是-1<x<1,则(a+b)2019= .19. 已知关于x的不等式组 只有四个整数解,则实数a的取值范是 .20. 在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于 .三、解答题
-
21.(1)、解方程组: .(2)、解不等式组: .22. 如图, , 是旧河道 两旁的两个村庄.为方便村民饮水,计划在旧河道 上打一口水井 ,用管道引水到两村,要求该井到两村的距离相等,请用尺规在图中作出点 的位置(保留作图痕迹,不要求写作法).
 23. 如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作 、 ,把 、 作为点 的横、纵坐标.
23. 如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作 、 ,把 、 作为点 的横、纵坐标. (1)、写出点 所有可能的坐标;(2)、求点 在直线 上的概率.24. 如图,在 中, , , 是一条角平分线.
(1)、写出点 所有可能的坐标;(2)、求点 在直线 上的概率.24. 如图,在 中, , , 是一条角平分线.求证: .
 25. 在共建美好家园活动中,校团委把一批树苗分给九年级(1)班同学去栽种,如果每人分2棵,还剩42棵,如果每人分3棵,那么最后一个人得到的树苗少于5棵,(但至少分的一棵),问九年级(1)班至少有多少学生?至多有多少学生?26. 如图,直线 : 与直线 : 相交于点 .
25. 在共建美好家园活动中,校团委把一批树苗分给九年级(1)班同学去栽种,如果每人分2棵,还剩42棵,如果每人分3棵,那么最后一个人得到的树苗少于5棵,(但至少分的一棵),问九年级(1)班至少有多少学生?至多有多少学生?26. 如图,直线 : 与直线 : 相交于点 . (1)、求关于 , 的方程组 的解;(2)、已知直线 经过第一、二、四象限,则当 时, .27. 如图,求证: .
(1)、求关于 , 的方程组 的解;(2)、已知直线 经过第一、二、四象限,则当 时, .27. 如图,求证: .
