四川省达州市渠县2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 不等式8﹣4x≥0的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
2. 下列各等式成立的是（）

A、 $\frac{b^{2}}{a^{2}} = \frac{b}{a}$ B、 $\frac{a^{2} - b^{2}}{a - b} = a - b$ C、 $\frac{a^{2} + 2 a + 1}{a + 1} = a + 1$ D、 $\frac{3 x - 4 y}{8 x y - 6 x^{2}} = \frac{1}{2 x}$

查看试题解析
3. 如果代数式4x²+kx+25能够分解成（2x﹣5）²的形式，那么k的值是（）

A、10 B、﹣20 C、±10 D、±20

查看试题解析
4. 如图，把三角形ABC沿直线BC方向平移得到三角形DEF，则下列结论错误的是（）

A、∠A＝∠D B、BE＝CF C、AC＝DE D、AB∥DE

查看试题解析
5. 如图，将△ABC绕点A旋转至△ADE的位置，使点E落在BC边上，则对于结论：①DE＝BC；②∠EAC＝∠DAB；③EA平分∠DEC；④若DE∥AC，则∠DEB＝60°；其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 如图，在已知的△ABC中，按以下步骤作图：①分别以A，B为圆心，以大于 $\frac{1}{2}$ AB的长为半径作弧，两弧相交于两点EF；②作直线EF交BC于点D连接AD．若AD＝AC，∠C＝40°，则∠BAC的度数是（）

A、105° B、110° C、I15° D、120°

查看试题解析
7. 利用一次函数y＝kx+b（k≠0）的图象解关于x的不等式kx+b≤0，若它的解集是x≥﹣2，则一次函数y＝kx+b的图象为（）

A、 B、 C、 D、

查看试题解析
8. 如图，在四边形ABCD中，对角线AC，BD相交于点O，AB∥CD，添加下列条件不能使四边形ABCD成为平行四边形的是（）

A、AB＝CD B、OB＝OD C、∠BCD+∠ADC＝180° D、AD＝BC

查看试题解析
9. 已知关于x的不等式组 ${\begin{array}{l} 2 x - 4 ⩾ 0 \\ 1 + x < a \end{array}$ 无解，则a的取值范围是（）

A、a＜3 B、a≤3 C、a＞3 D、a≥3

查看试题解析
10. 如图，在平行四边形ABCD中，AE平分∠BAD，交BC于点E且AB＝AE，延长AB与DE的延长线相交于点F，连接AC、CF．下列结论：①△ABC≌△EAD；②△ABE是等边三角形；③BF＝AD；④S_△_BEF＝S_△_ABC；⑤S_△_CEF＝S_△_ABE；其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

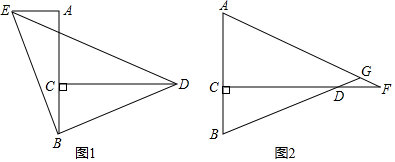
11. 如图，在Rt△ABC中，BD平分∠ABC交AC于点D，过D作DE∥BC交AB于点E，若DE刚好平分∠ADB，且AE＝a，则BC＝．

查看试题解析
12. 对于实数x我们规定[x]表示不大于x的最大整数，例如[1.8]＝1，[7]＝7，[﹣5]＝﹣5，[﹣2.9]＝﹣3，若[ $\frac{x - 3}{6}$ ]＝﹣2，则x的取值范围是．

查看试题解析
13. 如图，在△ABC中，∠ACB=90°，AC=4，BC=3，将△ABC绕点A顺时针旋转得到△ADE（其中点B恰好落在AC延长线上点D处，点C落在点E处），连接BD，则四边形AEDB的面积为．

查看试题解析
14. 分解因式：﹣2x²y+16xy﹣32y= ．

查看试题解析
15. 不改变分式的值，使分子、分母的第一项系数都是正数，则 $\frac{- 2 x + y}{- x - 3 y}$ ＝．

查看试题解析
16. 如图，在△ABC中，AB＝AC，E，F分别是BC，AC的中点，以AC为斜边作Rt△ADC，若∠CAD＝∠BAC＝45°，则下列结论：①CD∥EF；②EF＝DF；③DE平分∠CDF；④∠DEC＝30°；⑤AB＝ $\sqrt{2}$ CD；其中正确的是（填序号）

查看试题解析

三、解答题

17. 解不等式（组），并把解集在数轴上表示出来

(1)、 $\frac{x + 1}{2} > \frac{x - 1}{3}$

(2)、 ${\begin{array}{l} 3 (x - 3) < 5 x - 5 \\ \frac{3 x + 1}{5} \geq x - 1 \end{array}$

查看试题解析
18.

(1)、计算：4037²﹣4×2018×2019；

(2)、将边长为1的一个正方形和一个底边为1的等腰三角形如图摆放，求△ABC的面积．

查看试题解析
19. 先化简，再求值 $\frac{a^{2} - 6 a b + 9 b^{2}}{a^{2} - 2 a b} \div (\frac{5 b^{2}}{a - 2 b} - a - 2 b) - \frac{1}{a}$ ，其中a＝3，b＝﹣2．

查看试题解析
20. 某学校为了美化绿化校园，计划购买甲，乙两种花木共100棵绿化操场，其中甲种花木每棵60元，乙种花木每棵80元．

(1)、若购买甲，乙两种花木刚好用去7200元，则购买了甲，乙两种花木各多少棵？

(2)、如果购买乙种花木的数量不少于甲种花木的数量，请设计一种购买方案使所需费用最低，并求出该购买方案所需总费用．

查看试题解析
21. 某工厂制作AB两种型号的环保包装盒．已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个，且制作一个A型盒比制作一个B型盒要多用20%的材料．求制作每个A，B型盒各用多少材料？

查看试题解析
22. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）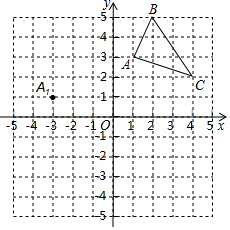

(1)、将△ABC平移，使点A移动到点A₁ ，请画出△A₁B₁C₁；

(2)、作出△ABC关于O点成中心对称的△A₂B₂C₂ ，并直接写出A₂ ， B₂ ， C₂的坐标；

(3)、△A₁B₁C₁与△A₂B₂C₂是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由．

查看试题解析
23. 如图，在△ABC中，点D是AB的中点，点F是BC延长线上一点，连接DF，交AC于点E，连接BE，∠A＝∠ABE

(1)、求证：ED平分∠AEB；

(2)、若AB＝AC，∠A＝38°，求∠F的度数．

查看试题解析
24. 如图，等边△ABC的边长是2，D，E分别是AB，AC的中点，延长BC至点F，使CF＝ $\frac{1}{2}$ BC，连接CD，EF

(1)、求证：CD＝EF；

(2)、求EF的长．

查看试题解析
25. 如图1，已知AB⊥CD，C是AB上一动点，AB＝CD

(1)、在图1中，将BD绕点B逆时针方向旋转90°到BE，若连接DE，则△DBE为等腰直角三角形；若连接AE，试判断AE与BC的数量和位置关系并证明；

(2)、如图2，F是CD延长线上一点，且DF＝BC，直线AF，BD相交于点G，∠AGB的度数是一个固定值吗？若是，请求出它的度数；若不是，请说明理由．

查看试题解析