浙江省绍兴市平水镇2020年数学中考模拟试卷(5月)
试卷更新日期:2020-06-23 类型:中考模拟
一、一.选择题(共10小题,满分40分,每小题4分)
-
1. 下列各数中,最大的是( )A、-0.5 B、-0.55 C、-0.05 D、-0.5552. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算结果正确的是( )A、2x+3y=5xy B、(m+2)2=m2+4 C、(xy2)
3. 下列运算结果正确的是( )A、2x+3y=5xy B、(m+2)2=m2+4 C、(xy2) =xy6
D、a10÷a5=a5
4. 如图所示的几何体是由
=xy6
D、a10÷a5=a5
4. 如图所示的几何体是由 个大小相同的小立方块搭成,它的俯视图是( )
个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下图:
5. 学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下图:售价
3元
4元
5元
6元
数目
14本
11本
10本
15本
下列说法正确的是( )
A、该班级所售图书的总数收入是226元 B、在该班级所售图书价格组成的一组数据中,中位数是4 C、在该班级所售图书价格组成的一组数据中,众数是15 D、在该班级所售图书价格组成的一组数据中,方差是26. 如图,在平面直角坐标系中,点A,B,C的坐标分别为(-1,3)、(-4,1)、(-2,1),将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),则点A1 , C1的坐标分别是( ) A、A1(4,4),C1(3,2) B、A1(3,3),C1(2,1) C、A1(4,3),C1(2,3) D、A1(3,4),C1(2,2)7. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则弧CF的长为( )
A、A1(4,4),C1(3,2) B、A1(3,3),C1(2,1) C、A1(4,3),C1(2,3) D、A1(3,4),C1(2,2)7. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则弧CF的长为( ) A、 B、 C、 D、π8. "桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客a万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加b% ,则可列方程为( )A、a(1+5%)(1+b%)=a(1+8%×2) B、a(1+5%)(1+b%)=a(1+8%)2 C、a(1+5%)(1+8%)=a(1+b%×2) D、a(1+5%)(1+8%)=2a(1+b%)29. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )
A、 B、 C、 D、π8. "桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客a万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加b% ,则可列方程为( )A、a(1+5%)(1+b%)=a(1+8%×2) B、a(1+5%)(1+b%)=a(1+8%)2 C、a(1+5%)(1+8%)=a(1+b%×2) D、a(1+5%)(1+8%)=2a(1+b%)29. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )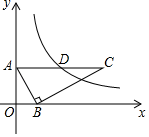 A、4 B、5 C、6 D、810. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )
A、4 B、5 C、6 D、810. 如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P , 点B与点O重合,且AC大于OE , 将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x , 则x的取值范围是( )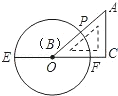 A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤120
A、30≤x≤60 B、30≤x≤90 C、30≤x≤120 D、60≤x≤120二、二.填空题(共6小题,满分30分,每小题5分)
-
11. 已知m是4的相反数,n比m的相反数小2,则m-n等于 .12. 庚子新春,一场突如其来的新冠肺炎疫情肆虐湖北。举国上下,众志成城,为坚决打赢疫情防控的人民战争、总体战、阻击战,截止2020年2月28日,国家卫健委组织支援湖北的医护人员已超过40000人。数字40000用科学记数法表示为。13. 分解因式:ax2-6axy+9ay2= .14. 现有形状大小一样、背面相同的五张卡片,在它们的正面分别标有数字0,1,2,3,6.若把五张卡片背面朝上,洗匀放在桌子上,然后任意抽取一张卡片,不放回,再任意抽取一张卡片,则抽取的两张卡片上的数字的积不大于2的概率是.15. 如图,四边形ABCD中,CD=AD,∠CDA=∠ABD=90°,点E为CD边的中点,连接BE,AB=2,BC=
 ,则BD=。
,则BD=。
 16. 矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为.
16. 矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为.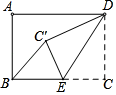
三、三.解答题(共8小题,满分80分)
-
17. 计算:(1)、计算:|﹣3|+tan60°+ ;(2)、化简:(x﹣1)2+x(x+1).18. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动。为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它"四种类型的设备对学生做了一次抽样调查。调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
 (1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.19. 如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
(1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.19. 如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.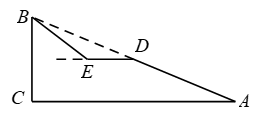
(参考三角函数:sin37°≈ ,cos37°≈ ,tan37°≈ )
(1)、求斜坡的高度BC.(2)、现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.20. 某商店准备购进A, B两种商品,A种商品每件的进价比B种商品每件的进价多20元,用3000元购进A种商品和用1800元购进B种商品的数量相同.商店将A种商品
每件的售价定为80元,B种商品每件的售价定为45元.
(1)、A种商品每件的进价和B种商品每件的进价各是多少元?(2)、商店计划用不超过1560元的资金购进 两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案?(3)、端午节期间,商店开展优惠促销活动,决定对每件A种商品售价优惠M( )元,B种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.21. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.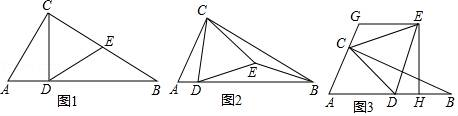 (1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.22. 小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁)。如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函数表达式为y=kx+6。
(1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.22. 小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁)。如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函数表达式为y=kx+6。 (1)、求小明骑公共自行车的速度;(2)、求线段CD对应的函数表达式:(3)、求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?23. 如图,△ABC 中,∠ACB=90°,BC=6,AC=8. 点E与点B在 AC 的同侧,且AE⊥AC .
(1)、求小明骑公共自行车的速度;(2)、求线段CD对应的函数表达式:(3)、求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?23. 如图,△ABC 中,∠ACB=90°,BC=6,AC=8. 点E与点B在 AC 的同侧,且AE⊥AC .
 (1)、如图1,点E不与点A重合,连结CE交AB于点P.设AE=x,AP=y,求y关于x的函数解析式,写出自变量x的取值范围;(2)、是否存在点E,使△PAE与△ABC 相似,若存在,求AE的长;若不存在,请说明理由;(3)、如图2,过点B作BD⊥AE,垂足为D .将以点E为圆心, ED为半径的圆记为⊙E .若点C到OE上点的距离的最小值为8,求⊙E的半径.24. 如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.
(1)、如图1,点E不与点A重合,连结CE交AB于点P.设AE=x,AP=y,求y关于x的函数解析式,写出自变量x的取值范围;(2)、是否存在点E,使△PAE与△ABC 相似,若存在,求AE的长;若不存在,请说明理由;(3)、如图2,过点B作BD⊥AE,垂足为D .将以点E为圆心, ED为半径的圆记为⊙E .若点C到OE上点的距离的最小值为8,求⊙E的半径.24. 如图,在平面直角坐标系xOy中,将抛物线y=﹣x2+bx+c与直线y=﹣x+1相交于点A(0,1)和点B(3,﹣2),交x轴于点C,顶点为点F,点D是该抛物线上一点.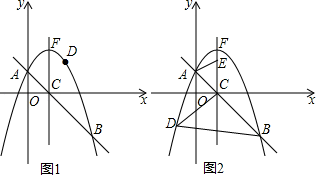 (1)、求抛物线的函数表达式;(2)、如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)、如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.
(1)、求抛物线的函数表达式;(2)、如图1,若点D在直线AB上方的抛物线上,求△DAB的面积最大时点D的坐标;(3)、如图2,若点D在对称轴左侧的抛物线上,且点E(1,t)是射线CF上一点,当以C、B、D为顶点的三角形与△CAE相似时,求所有满足条件的t的值.