四川省成都市武侯区2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 据益阳气象部门记载，2018年6月30日益阳市最高气温是33℃，最低气温是24℃，则当天益阳市气温 $t$ （℃）的变化范围是（）

A、 $t > 33$ B、 $t \leq 24$ C、 $24 < t < 33$ D、 $24 \leq t \leq 33$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列分解因式正确的是（）

A、x²-x+2=x（x-1）+2 B、x²-x=x（x-1） C、x-1=x（1- $\frac{1}{x}$ ） D、（x-1）²=x²-2x+1

查看试题解析
4. 函数 $y = \frac{2 x}{x + 1}$ 中，自变量x的取值范围是（）

A、x＞-1 B、x＞1 C、x≠-1 D、x≠0

查看试题解析
5. 点P（﹣3，m+1）在第二象限，则m的取值范围在数轴上表示正确的是（）

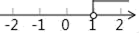A、 B、 C、 D、

查看试题解析
6. 已知 $4 x^{2} + m x + 9$ 是完全平方式，则 $m$ 的值为（）

A、6 B、 $\pm 6$ C、12 D、 $\pm 12$

查看试题解析
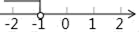7. 下列命题为真命题的是（）

A、若ab＞0，则a＞0，b＞0 B、两个锐角分别相等的两个直角三角形全等 C、在一个角的内部，到角的两边距离相等的点在这个角的平分线上 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为（）

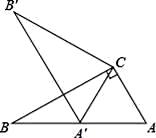A、30° B、60° C、90° D、150°

查看试题解析
9. 武侯区某学校计划选购甲，乙两种图书为“初中数学分享学习课堂之生讲生学”初赛的奖品．已知甲图书的单价是乙图书单价的1.5倍，用600元单独购买甲种图书比单独购买乙种图书少10本，设乙种图书的价为x元，依据题意列方程正确的是（）

A、 $\frac{600}{x} - \frac{600}{1.5 x} = 10$ B、 $\frac{600}{1.5 x} - \frac{600}{x} = 10$ C、 $\frac{600}{x + 10} - \frac{600}{x} = 1.5$ D、 $\frac{600}{x} - \frac{600}{x + 10} = 1.5$

查看试题解析
10. 已知AB=8cm，小红在作线段AB的垂直平分线时操作如下：分别以A和B为圆心，5cm的长为半径画弧，两弧相交于C、D，则直线CD即为所求，根据此种作图方法所得到的四边形ADBC的面积是（）

A、12cm² B、24cm² C、36cm² D、48cm²

查看试题解析

二、填空题

11. 分解因式：x³-3x= ．

查看试题解析
12. 某数学学习小组发现：通过连多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题．如果从某个多边形的一个顶点出发的对角钱共有3条，那么该多边形的内角和是度．

查看试题解析
13. 已知 $\frac{1}{a} - \frac{1}{b} = \frac{1}{3}$ ，则 $\frac{a b}{b - a}$ 的值等于.

查看试题解析
14.
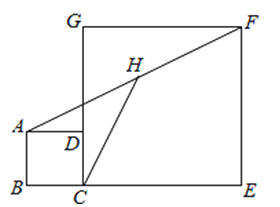
如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是．

查看试题解析
15. 若a+b＝4，a﹣b＝1，则（a+2）²﹣（b﹣2）²的值为．

查看试题解析
16. 关于t的分式方程 $\frac{m}{t - 2} + \frac{5}{2 - t}$ =1的解为负数，则m的取值范围是．

查看试题解析
17. 若直线l₁：y₁=k₁x+b₁经过点（0，3），l₂：y₂=k₂x+b₂经过点（3，1），且l₁与l₂关于x轴对称，则关于x的不等式k₁x+b₁＞k₂x+b₂的解集为．

查看试题解析
18. 如图，在直角坐标系中，正方形OABC顶点B的坐标为（6，6），直线CD交直线OA于点D，直线OE交线段AB于点E，且CD⊥OE，垂足为点F，若图中阴影部分的面积是正方形OABC的面积的 $\frac{1}{3}$ ，则△OFC的周长为．

查看试题解析
19. 如图，△ABC，△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，将△ADE绕点A在平面内自由旋转，连接DC，点M，P，N分别为DE，DC，BC的中点，若AD=3，AB=7，则线段MN的取值范围是．

查看试题解析

三、解答题

20. 计算

(1)、分解因式：a²-b²+ac-bc

(2)、解不等式组 ${\begin{matrix} 2 (x - 1) \leq x + 1 \\ \frac{x + 2}{2} \geq \frac{x + 3}{3} \end{matrix}$ ，并求出不等式组的整数解之和．

查看试题解析
21. 如图，在四边形ABCD中，AB=CD，DE⊥AC，BF⊥AC，垂足分别为E，F，且DE=BF，求证：

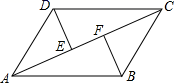(1)、AE=CF；

(2)、四边形ABCD是平行四边形．

查看试题解析
22. 对于任意三个实数a，b，c，用min|a，b，c|表示这三个实数中最小数，例如：min|-2，0，1|=-2，则：

(1)、填空，min|（-2019）⁰ ，（- $\frac{1}{2}$ ）^-2 ， - $\sqrt{3}$ |= ，如果min|3，5-x，3x+6|=3，则x的取值范围为；

(2)、化简： $\frac{x - 1}{x - 2}$ ÷（x+2+ $\frac{3}{x - 2}$ ）并在（1）中x的取值范围内选取一个合适的整数代入求值．

查看试题解析
23. 如图，在边长为1个单位长度的小正方形组成的网络中，给出了△ABC和△DEF（网点为网格线的交点）

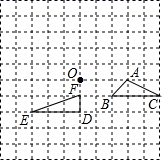(1)、将△ABC向左平移两个单位长度，再向上平移三个单位长度，画出平移后的图形△A₁B₂C₃；

(2)、画出以点O为对称中心，与△DEF成中心对称的图形△D₂E₂F₂；

(3)、求∠C+∠E的度数．

查看试题解析
24. 如图，在△ABC中，∠ABC=90°，将△ABC绕点C顺时针旋转得到△DEC，连接AD，BE，延长BE交AD于点F．

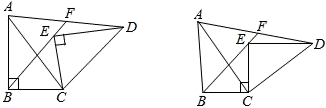(1)、求证：∠DEF=∠ABF；

(2)、求证：F为AD的中点；

(3)、若AB=8，AC=10，且EC⊥BC，求EF的长．

查看试题解析
25. 2019车8月8日至18日，第十八届“世警会”首次来到亚洲在成都举办武侯区以相关事宜为契机，进一步改善区域生态环境．在天府吴园道部分地段种植白芙蓉和醉芙蓉两种花卉．经市场调查，种植费用y（元）与种植面积x（m²）之间的函数关系如图所示．

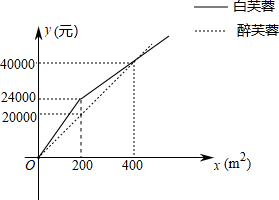(1)、求出两种花卉y与x的函数关系式；

(2)、白芙蓉和醉芙蓉两种花卉的种植面积共1000m² ，若白芙蓉的种植面积不少于100m²且不超过醉芙蓉种植面积的3倍，那么应该怎样分配两种花卉的种植面积才能使种植总费用最少？

查看试题解析
26. 在矩形ABCD中，AB=12，BC=25，P是线段AB上一点（点P不与A，B重合），将△PBC沿直线PC折叠，顶点B的对应点是点G，CG，PG分别交线段AD于E，O．

(1)、如图1，若OP=OE，求证：AE=PB；

(2)、如图2，连接BE交PC于点F，若BE⊥CG．
①求证：四边形BFGP是菱形；

②当AE=9，求 $\frac{BF}{PC}$ 的值．

查看试题解析
27. 如图，已知直线 $y = k x + 4 (k \neq 0)$ 经过点 $(- 1 ， 3)$ ，交x轴于点A ， y轴于点B ， F为线段AB的中点，动点C从原点出发，以每秒1个位长度的速度沿y轴正方向运动，连接FC ，过点F作直线FC的垂线交x轴于点D ，设点C的运动时间为t秒．

(1)、当 $0 < t < 4$ 时，求证： $F C = F D$ ；

(2)、连接CD ，若 $△ F D C$ 的面积为S ，求出S与t的函数关系式；

(3)、在运动过程中，直线CF交x轴的负半轴于点G ， $\frac{1}{0 C} + \frac{1}{0 G}$ 是否为定值？若是，请求出这个定值；若不是，请说明理由．

查看试题解析
28. 解分式方程： $\frac{x}{x - 2} + \frac{6}{x + 2} = 1$ .

查看试题解析