湖北省黄石市下陆区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、2. 若一个三角形的三边长为 ,则使得此三角形是直角三角形的的值是( )A、 B、 C、 D、 或3. 函数 y=ax﹣a 的大致图象是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 对角线相等且互相平分的四边形是( )A、一般四边形 B、平行四边形 C、矩形 D、菱形6. 某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )A、中位数 B、众数 C、平均数 D、极差7. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量 (升)与行驶时间 (小时)之间的函数关系的图象是( )A、
4. 下列计算正确的是( )A、 B、 C、 D、5. 对角线相等且互相平分的四边形是( )A、一般四边形 B、平行四边形 C、矩形 D、菱形6. 某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )A、中位数 B、众数 C、平均数 D、极差7. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量 (升)与行驶时间 (小时)之间的函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、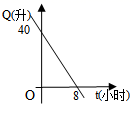 8. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )
8. 如图,函数 和 的图象相交于A(m,3),则不等式 的解集为( )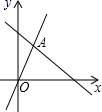 A、 B、 C、 D、9. 如图,菱形 中, ,点 是边 上一点,占 在 上,下列选项中不正确的是( )
A、 B、 C、 D、9. 如图,菱形 中, ,点 是边 上一点,占 在 上,下列选项中不正确的是( ) A、若 ,则 B、若 , 则 C、若 ,则 的周长最小值为 D、若 ,则10. 如图,在平行四边形 中, 是 边上的中点, 是 边上的一动点,将 沿 所在直线翻折得到 ,连接 ,则 的最小值为( )
A、若 ,则 B、若 , 则 C、若 ,则 的周长最小值为 D、若 ,则10. 如图,在平行四边形 中, 是 边上的中点, 是 边上的一动点,将 沿 所在直线翻折得到 ,连接 ,则 的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .
12. 一次函数 的图象不经过第象限.13. 从某市5000名初一学生中,随机地抽取100名学生,测得他们的身高数据,得到一个样本,则这个样本数据的平均数、中位数、众数、方差四个统计量中,服装厂最感兴趣的是.14. 若方程组 的解是 ,则直线y=﹣2x+b与直线y=x﹣a的交点坐标是.15. 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= BD,连接DM、DN、MN.若AB=6,则DN= . 16. 如图,在 中,角 是 边上的一点,作 垂直 , 垂直 ,垂足分别为 ,则 的最小值是.
16. 如图,在 中,角 是 边上的一点,作 垂直 , 垂直 ,垂足分别为 ,则 的最小值是.
三、解答题
-
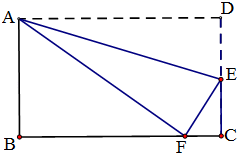
17. 计算: .18. 先化简,再求值:( ﹣ )÷ ,其中x= +1,y= ﹣1.19. 如图所示,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm.求CE的长?
 20. 已知y=y1+y2 , y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.(1)、求y与x的函数关系式,并说明此函数是什么函数;(2)、当x=3时,求y的值.21. 如图,DB∥AC,且DB= AC,E是AC的中点,
20. 已知y=y1+y2 , y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.(1)、求y与x的函数关系式,并说明此函数是什么函数;(2)、当x=3时,求y的值.21. 如图,DB∥AC,且DB= AC,E是AC的中点,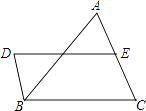 (1)、求证:BC=DE;(2)、连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?22. 某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
(1)、求证:BC=DE;(2)、连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?22. 某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.第1次
第2次
第3次
第4次
第5次
王同学
60
75
100
90
75
李同学
70
90
100
80
80
根据上表解答下列问题:
(1)、完成下表:姓名
平均成绩(分)
中位数(分)
众数(分)
方差
王同学
80
75
75
190
李同学
(2)、在这五次测试中,成绩比较稳定的同学是谁?若将80分以上的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?(3)、历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.23. 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
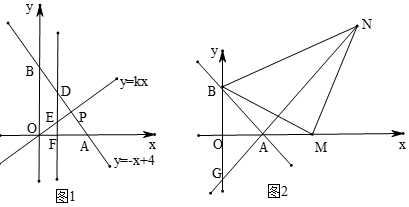
(1)、若购进这100件服装的费用不得超过7500,则甲种服装最多购进多少件?(2)、在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?24. 如图1,在正方形 中, 是对角线,点 在 上, 是等腰直角三角形,且 ,点 是 的中点,连结 与 . (1)、求证: .(2)、求证: .(3)、如图2,若等腰直角三角形 绕点 按顺时针旋转 ,其他条件不变,请判断 的形状,并证明你的结论.25. 如图1,已知直线 与坐标轴交于 两点,与直线 交于点 ,且 点的横坐标是纵坐标的 倍.(1)、求 的值.(2)、 为线段 上一点, 轴于点 ,交 于点 ,若 ,求 点坐标.(3)、如图2, 为 点右侧 轴上的一动点,以 为直角顶点, 为腰在第一象限内作等腰直角 ,连接 并延长交 轴于点 ,当 点运动时, 点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.
(1)、求证: .(2)、求证: .(3)、如图2,若等腰直角三角形 绕点 按顺时针旋转 ,其他条件不变,请判断 的形状,并证明你的结论.25. 如图1,已知直线 与坐标轴交于 两点,与直线 交于点 ,且 点的横坐标是纵坐标的 倍.(1)、求 的值.(2)、 为线段 上一点, 轴于点 ,交 于点 ,若 ,求 点坐标.(3)、如图2, 为 点右侧 轴上的一动点,以 为直角顶点, 为腰在第一象限内作等腰直角 ,连接 并延长交 轴于点 ,当 点运动时, 点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请说明理由.