湖北省大冶市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 要使代数式 有意义,则 的取值范围是A、 B、 C、 D、2. 以下列各组数为三角形的三边,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,233. 下列计算正确的是( )A、 B、 C、 =1 D、4. 如图,在△ 中, , , ,点 , 分别是边 , 的中点,那么 的长为( )
 A、1.5 B、2 C、3 D、45. 下列各式中,最简二次根式是( )A、 B、 C、 D、6. 某鞋店试销一款学生运动鞋,销量情况如图所示,鞋店经理要关心哪种型号的鞋是否畅销,下列统计量最有意义的是( )
A、1.5 B、2 C、3 D、45. 下列各式中,最简二次根式是( )A、 B、 C、 D、6. 某鞋店试销一款学生运动鞋,销量情况如图所示,鞋店经理要关心哪种型号的鞋是否畅销,下列统计量最有意义的是( )型号
22.5
23
23.5
24
24.5
销量(双)
5
10
15
8
3
A、平均数 B、中位数 C、众数 D、方差7. 关于函数y=2x,下列说法错误的是( )A、它是正比例函数 B、图象经过(1,2) C、图象经过一、三象限 D、当x>0,y<08. 关于四边形ABCD:①两组对边分别平行;②两组对边分别相等;③有一组对边平行且相等;④对角线AC和BD相等;以上四个条件中可以判定四边形ABCD是平行四边形的有( )A、1个 B、2个 C、3个 D、4个9. 将直线 向上平移1个单位长度,得到的一次函数解析式为A、 B、 C、 D、10.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
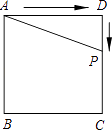 A、
A、 B、
B、 C、
C、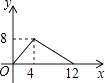 D、
D、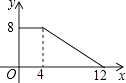
二、填空题
-
11. 计算: = .12. 甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是S甲2=0.4,S乙2=1.2,则成绩比较稳定的是 (填“甲”或“乙”)13. 已知一组数据3、x、4、8、6,若该组数据的平均数是5,则x的值是.14. 边长为2的等边三角形的面积为15. 如图,矩形ABCD的两条对角线相交于点O,若 , ,则AC的长为.
 16. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 , 、 、 在直线 上,点 、 、 在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、 ,则 的值为 用含n的代数式表示,n为正整数 .
16. 在直角坐标系中,直线 与y轴交于点 ,按如图方式作正方形 、 、 , 、 、 在直线 上,点 、 、 在x轴上,图中阴影部分三角形的面积从左到右依次记为 、 、 、 ,则 的值为 用含n的代数式表示,n为正整数 .
三、解答题
-
17. 计算:
;
18. 化简: ;19. 已知:如图,在平行四边形ABCD中,AE⊥BC,CF⊥AD,垂足分别为点E,点F.求证:BE=DF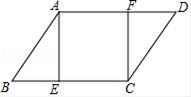 20. 下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
20. 下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:考试类别
平时考试
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩(分)
85
78
90
91
90
94
(1)、小明6次成绩的众数是 , 中位数是;(2)、求该同学这个同学这一学期平时成绩的平均数;(3)、总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?21. 如图,在正方形ABCD中,对角线AC,BD相较于点O, 的角平分线BF交CD于点E,交AC于点F (1)、求证: ;(2)、若 ,求AB的值22. 已知一次函数 的图象经过点 和(1)、求函数的解析式;(2)、求直线 上到x轴距离为4的点的坐标.23. 某文具店从市场得知如下信息:
(1)、求证: ;(2)、若 ,求AB的值22. 已知一次函数 的图象经过点 和(1)、求函数的解析式;(2)、求直线 上到x轴距离为4的点的坐标.23. 某文具店从市场得知如下信息:A品牌计算器
B品牌计算器
进价(元/台)
70
100
售价(元/台)
90
140
该文具店计划一次性购进这两种品牌计算器共50台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)、求y与x之间的函数关系式;(2)、若全部销售完后,获得的利润为1200元,则购进A、B两种品牌计算器的数量各是多少台?(3)、若购进计算器的资金不超过4100元,求该文具店可获得的最大利润是多少元?24. 如图,在 中,AD是BC边上的中线,点E是AD的中点,过点A作 交BE的延长线于F,BF交AC于G,连接CF. (1)、求证: ≌ ;(2)、若 ,试判断四边形ADCF的形状,并证明你的结论;(3)、求证: .25. 如图,在平面直角坐标系中,直线l1: 分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.
(1)、求证: ≌ ;(2)、若 ,试判断四边形ADCF的形状,并证明你的结论;(3)、求证: .25. 如图,在平面直角坐标系中,直线l1: 分别与x轴、y轴交于点B、C,且与直线l2: 交于点A.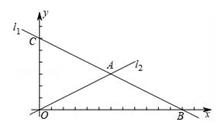 (1)、求出点A的坐标(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(1)、求出点A的坐标(2)、若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式(3)、在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.