四川省巴中市平昌县2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 下列说法错误的是( )A、当 时,分式 有意义 B、当 时,分式 无意义 C、不论 取何值,分式 都有意义 D、当 时,分式 的值为02. 下列等式成立的是( )A、 B、 C、 D、3. 若点P(a,a﹣2)在第四象限,则a的取值范围是( )A、﹣2<a<0 B、0<a<2 C、a>2 D、a<04. 把函数 与 的图象画在同一个直角坐标系中,正确的是( )A、
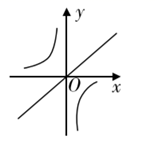 B、
B、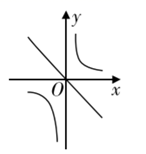 C、
C、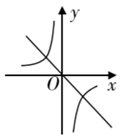 D、
D、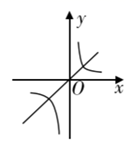 5. 下列命题,其中正确的有( )
5. 下列命题,其中正确的有( )①平行四边形的两组对边分别平行且相等
②平行四边形的对角线互相垂直平分
③平行四边形的对角相等,邻角互补
④平行四边形只有一组对边相等,一组对边平行
A、1个 B、2个 C、3个 D、4个6. 如图,四边形 是平行四边形,要使它变成菱形,需要添加的条件是( )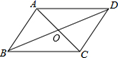 A、AC=BD B、AD=BC C、AB=BC D、AB=CD7. 下列条件中,不能判定四边形ABCD为菱形的是( ).A、AC⊥BD,AC与BD互相平分 B、AB=BC=CD=DA C、AB=BC,AD=CD,且AC⊥BD D、AB=CD,AD=BC,AC⊥BD8. 正方形具有而菱形不一定具有的性质是 ( )A、对角线相等 B、对角线互相垂直平分 C、四条边相等 D、对角线平分一组对角9. 为了解某公司员工的年工资情况,小王随机调查了10位员工,某年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20.下列统计量中,能合理反映该公司员工年工资水平的是( )A、方差 B、众数 C、中位数 D、平均数10. 甲,乙两个样本的容量相同,甲样本的方差为0.102,乙样本的方差是0.06,那么( )A、甲的波动比乙的波动大 B、乙的波动比甲的波动大 C、甲,乙的波动大小一样 D、甲,乙的波动大小无法确定
A、AC=BD B、AD=BC C、AB=BC D、AB=CD7. 下列条件中,不能判定四边形ABCD为菱形的是( ).A、AC⊥BD,AC与BD互相平分 B、AB=BC=CD=DA C、AB=BC,AD=CD,且AC⊥BD D、AB=CD,AD=BC,AC⊥BD8. 正方形具有而菱形不一定具有的性质是 ( )A、对角线相等 B、对角线互相垂直平分 C、四条边相等 D、对角线平分一组对角9. 为了解某公司员工的年工资情况,小王随机调查了10位员工,某年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20.下列统计量中,能合理反映该公司员工年工资水平的是( )A、方差 B、众数 C、中位数 D、平均数10. 甲,乙两个样本的容量相同,甲样本的方差为0.102,乙样本的方差是0.06,那么( )A、甲的波动比乙的波动大 B、乙的波动比甲的波动大 C、甲,乙的波动大小一样 D、甲,乙的波动大小无法确定二、填空题
-
11. 分式 的最简公分母为 .12. 函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k= , b=.13. 在四边形 中,给出下列条件:① ② ③ ④
其中能判定四边形是平行四边形的组合是或 或或 .
14. 如图所示,在正方形 中,延长 到点 ,若 ,则四边形 周长为 .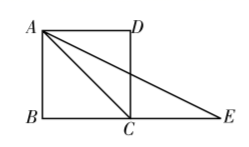 15. 小明五次测试成绩为:91、89、88、90、92,则五次测试成绩平均数为 , 方差为 .
15. 小明五次测试成绩为:91、89、88、90、92,则五次测试成绩平均数为 , 方差为 .三、解答题
-
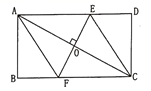
16. 计算与化简:(1)、计算:(2)、化简:(3)、已知 ,求: 的值17. 解分式方程: +3.18. 已知等腰三角形的周长为 , 底边长 是腰长 的函数.(1)、写出这个函数关系式;(2)、求自变量 的取值范围;(3)、画出这个函数的图象.19. 已知一个一次函数的图象与一个反比例函数的图象交于点 .(1)、分别求出这两个函数的表达式;(2)、在同一个平面直角坐标系中画出这两个函数的图象,根据图象回答:当 取何值时,一次函数的值大于反比例函数的值?(3)、求平面直角坐标中原点 与 点构成的三角形的面积.20. 合肥某单位计划组织员工外出旅游,人数估计在10~25人之间.甲、乙两旅行社的服务质量都较好,且旅游的价格都是每人200元.该单位联系时,甲旅行社表示可以给予每位旅客7.5折优惠,乙旅行社表示可免去一带队领导的旅游费用,其他游客8折优惠.问该单位怎样选择,可使其支付的旅游总费用较少?21. 有一个四边形的四边长分别是 ,且有 .求证:此四边形 是平行四边形.22. 如图,矩形 的对角线 垂直平分线与边 、 分别交于点 ,求证:四边形 为菱形.
 23. 如图,四边形 是正方形,点 是 上的任意一点, 于点 ,交 于点 .求证:
23. 如图,四边形 是正方形,点 是 上的任意一点, 于点 ,交 于点 .求证: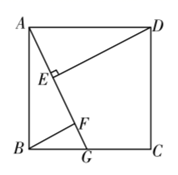 24. 八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
24. 八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成A,B,C,D,E五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.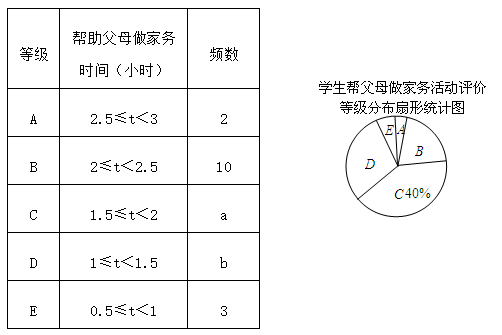 (1)、求a,b的值;(2)、根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;(3)、该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.25. 由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.(1)、求两队单独完成此项工程各需多少天?(2)、此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
(1)、求a,b的值;(2)、根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;(3)、该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.25. 由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.(1)、求两队单独完成此项工程各需多少天?(2)、此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?