山东省枣庄市滕州市2018-2019学年八年级下学期数学期末试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个著名数学图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将下列多项式因式分解，结果中不含因式x－1的是（）

A、x²－1 B、x²＋2x＋1 C、x²－2x＋1 D、x（x－2）＋（2－x）

查看试题解析
3. 无论a取何值时，下列分式一定有意义的是（）

A、 $\frac{a^{2} + 1}{a^{2}}$ B、 $\frac{a + 1}{a^{2}}$ C、 $\frac{a^{2} - 1}{a + 1}$ D、 $\frac{a - 1}{a^{2} + 1}$

查看试题解析
4. 若分式 $\frac{x^{2}}{x + 1}$ 口 $\frac{x}{x + 1}$ ，的运算结果为x（x≠0），则在“口”中添加的运算符号为（）

A、+或x B、-或÷ C、+或÷ D、-或x

查看试题解析
5. 如图，已知△ABC中，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）

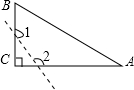A、90° B、135° C、270° D、315°

查看试题解析
6. 若平行四边形的一边长为7，则它的两条对角线长可以是（）

A、12和2 B、3和4 C、14和16 D、4和8

查看试题解析
7. 分式方程 $\frac{x}{x - 1} - 1 = \frac{m}{(x - 1) (x + 2)}$ 有增根，则 $m$ 的值为（）

A、0和3 B、1 C、1和 $- 2$ D、3

查看试题解析
8. 如图所示，在直角坐标系内，原点O恰好是▱ABCD对角线的交点，若A点坐标为（2，3），则C点坐标为（）

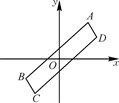A、（－3，－2） B、（－2，3） C、（－2，－3） D、（2，－3）

查看试题解析
9. 如图，在△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线分别交AB，AC于点D，E，则下列结论正确的是（）

A、AE＝3CE B、AE＝2CE C、AE＝BD D、BC＝2CE

查看试题解析
10. ▱ABCD中，E，F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是（）

A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF

查看试题解析
11. 下列命题正确的个数是（）
⑴若x²+kx+25是一个完全平方式，则k的值等于10；（2）正六边形的每个内角都等于相邻外角的2倍；（3）一组对边平行，一组对角相等的四边形是平行四边形；（4）顺次连结四边形的四边中点所得的四边形是平行四边形

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）

A、66° B、104° C、114° D、124°

查看试题解析
13. 小明乘出租车去体育场，有两条路线可供选择：路线一的全程是25千米，但交通比较拥堵，路线二的全程是30千米，平均车速比走路线一时的平均车速能提高80%，因此能比走路线一少用10分钟到达．若设走路线一时的平均速度为x千米/小时，根据题意，得（）

A、 $\frac{25}{x} - \frac{30}{(1 + 80 %) x} = \frac{10}{60}$ B、 $\frac{25}{x} - \frac{30}{(1 + 80 %) x} = 10$ C、 $\frac{30}{(1 + 80 %) x} - \frac{25}{x} = \frac{10}{60}$ D、 $\frac{30}{(1 + 80 %) x} - \frac{25}{x} = 10$

查看试题解析
14. 如图，设甲图中阴影部分的面积为S₁ ，乙图中阴影部分的面积为S₂ ， k= $\frac{S_{1}}{S_{2}}$ （a＞b＞0），则有（）

A、k＞2 B、1＜k＜2 C、 $\frac{1}{2}$ ＜k＜1 D、0＜k＜ $\frac{1}{2}$

查看试题解析
15. 如图，∠AOB是一钢架，∠AOB＝15°，为使钢架更加牢固，需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等，则最多能添加这样的钢管（）根．

A、2 B、4 C、5 D、无数

查看试题解析

二、填空题

16. 已知不等式组 ${\begin{array}{l} 2 x - a < 1 \\ x - 2 b > 3 \end{array}$ 的解集是 $- 1 < x < 1$ ，则 $(a + 1) (b + 1)$ 的值是的．

查看试题解析
17. 如图，在△ABC中，∠B＝32°，∠BAC的平分线AD交BC于点D，若DE垂直平分AB，则∠C的度数为．

查看试题解析
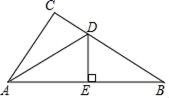18. 对于非零的两个实数a、b，规定a⊕b= $\frac{1}{b} - \frac{1}{a}$ ，若2⊕（2x﹣1）=1，则x的值为．

查看试题解析
19. 如图，▱ABCD的对角线AC、BD相交于点O，E是AB中点，且AE+EO＝4，则▱ABCD的周长为．

查看试题解析
20. 如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分，正多边形①和②的内角都是108°，则正多边形③的边数是．

查看试题解析
21. 如图，平行四边形ABCD的面积为32，对角线BD绕着它的中点O按顺时针方向旋转一定角度后，其所在直线分别交BC，AD于点E、F，若AF＝3DF，则图中阴影部分的面积等于

查看试题解析

三、解答题

22.

(1)、因式分解：9（m+n）²﹣（m﹣n）²

(2)、已知：x+y＝1，求 $\frac{1}{2}$ x²+xy+ $\frac{1}{2}$ y²的值．

查看试题解析
23.

(1)、解方程： $\frac{x}{2 x - 3}$ + $\frac{5}{3 - 2 x}$ ＝4

(2)、解不等式组并把解集表示在数轴上： ${\begin{cases} \frac{3 x - 1}{2} - \frac{2 x + 1}{3} \leq 6 ① \\ 2 x + 1 < 3 （ x - 1 ） ② \end{cases}$ .

查看试题解析
24. 先化简（ $\frac{m^{2} + 4 m}{m - 2}$ -m-2）÷ $\frac{m^{2} + 2 m + 1}{m - 2}$ ，然后从-2＜m≤2中选一个合适的整数作为m的值代入求值．

查看试题解析
25. 先阅读下列材料，再解答下列问题：
材料：因式分解：（x＋y）²＋2（x＋y）＋1.

解：将“x＋y”看成整体，令x＋y＝A，则

原式＝A²＋2A＋1＝（A＋1）².

再将“A”还原，得原式＝（x＋y＋1）².

上述解题用到的是“整体思想”，“整体思想”是数学解题中常用的一种思想方法，请你解答下列问题：

(1)、因式分解：1＋2（x－y）＋（x－y）²＝；

(2)、因式分解：（a＋b）（a＋b－4）＋4；

(3)、求证：若n为正整数，则式子（n＋1）（n＋2）（n²＋3n）＋1的值一定是某一个整数的平方．

查看试题解析
26. 如图，在▱ABCD中，∠ABC的平分线交AD于点E，延长BE交CD的延长线于点F.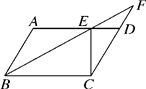

(1)、若∠F＝20°，求∠A的度数；

(2)、若AB＝5，BC＝8，CE⊥AD，求▱ABCD的面积．

查看试题解析
27. 明德中学在商场购买甲、乙两种不同足球，购买甲种足球共花费3000元，购买乙种足球共花费2100元，购买甲种足球数量是购买乙种足球数量的2倍．且购买一个乙种足球比购买一个甲种足球多花20元．

(1)、求购买一个甲种足球、一个乙种足球各需多少元；

(2)、为响应国家“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个，恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%．如果此次购买甲、乙两种足球的总费用不超过2950元，那么这所学校最多可购买多少个乙种足球？

查看试题解析
28. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB=3cm，BC=5cm．点P从A点出发沿AD方向匀速运动速度为lcm/s，连接PO并延长交BC于点Q．设运动时间为t（s）（0＜t＜5）

(1)、当t为何值时，四边形ABQP是平行四边形？

(2)、设四边形OQCD的面积为y（cm²），当t=4时，求y的值．

查看试题解析