河南省开封市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-06-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（　　）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{5}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
2. 下列各组数中，可以组成直角三角形的是（　　）

A、1：2：3 B、2，3，4 C、3，4，5 D、3² ， 4² ， 5²

查看试题解析
3. 下列计算正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{2} - \sqrt{2} = 2$ C、 $2 + \sqrt{6} = 2 \sqrt{6}$ D、 $\sqrt{(- 4) \times (- 2)} = 2 \sqrt{2}$

查看试题解析
4. 汽车在匀速行驶过程中，路程s、速度v、时间t之间的关系为 $s = v t$ ，下列说法正确的是（）

A、s、v、t都是变量 B、s、t是变量，v是常量 C、v、t是变量，s是常量 D、s、v是变量、t是常量

查看试题解析
5. 数据 0，1，1，3，3，4 的中位数和平均数分别是（）

A、2和2.4 B、2和2 C、1和2 D、3和2

查看试题解析
6. 正比例函数y＝2x的图象必经过点（　　）

A、（﹣1，﹣2） B、（﹣1，2） C、（1，﹣2） D、（2，1）

查看试题解析
7. 已知点 $A (- 2, y_{1})$ ， $B (1, y_{2})$ 都在直线 $y = - 2 x + 2$ 上，则y₁、y₂的大小关系是（）

A、 $y_{1} = y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} > y_{2}$ D、 $y_{1} \geq y_{2}$

查看试题解析
8. 如图，菱形ABCD的对角线AC，BD的长分别为6cm，8cm，则这个菱形的周长为（）

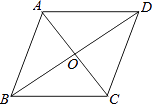A、5cm B、10cm C、14cm D、20cm

查看试题解析
9. 在▱ABCD中，已知AB＝6，BE平分∠ABC交AD边于点E，点E将AD分为1：3两部分，则AD的长为（　　）

A、8或24 B、8 C、24 D、9或24

查看试题解析
10. 正方形ABCD，正方形CEFG如图放置，点B，C，E在同一条直线上，点P在BC边上，PA＝PF，且∠APF＝90°，连接AF交CD于点M.有下列结论：①EC＝BP；②AP＝AM：③∠BAP＝∠GFP；④AB²+CE²＝ $\frac{1}{2}$ AF²；⑤S_正方形_ABCD+S_正方形_CGFE＝2S_△_APF ，其中正确的是（　　）

A、①②③ B、①③④ C、①②④⑤ D、①③④⑤

查看试题解析

二、填空题

11. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是.

查看试题解析
12. 某生产小组6名工人某天加工零件的个数分别是10，10，11，12，8，10，则这组数据的众数为.

查看试题解析
13. 把直线 $y = 2 x + 3$ 向下平移2个单位长度，得到直线的解析式是.

查看试题解析
14. 矩形两条对角线的夹角为60°，对角线长为14，则该矩形较长的边长为.

查看试题解析
15.
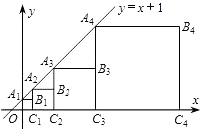
如图所示，直线y=x+1与y轴相交于点A₁ ，以OA₁为边作正方形OA₁B₁C₁ ，记作第一个正方形；然后延长C₁B₁与直线y=x+1相交于点A₂ ，再以C₁A₂为边作正方形C₁A₂B₂C₂ ，记作第二个正方形；同样延长C₂B₂与直线y=x+1相交于点A₃ ，再以C₂A₃为边作正方形C₂A₃B₃C₃ ，记作第三个正方形；…，依此类推，则第n个正方形的边长为．

查看试题解析

三、解答题

16. 计算：

(1)、 $(\sqrt{24} - \sqrt{\frac{1}{2}}) - (\sqrt{\frac{1}{8}} + \sqrt{6})$ ；

(2)、 $(3 \sqrt{2} + \sqrt{3}) (3 \sqrt{2} - \sqrt{3})$

查看试题解析
17. 如图，《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺，问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹稍恰好抵地，抵地处离竹子底部6尺远，求折断处离地面的高度．

查看试题解析
18. 如图， $▱ A B C D$ 的对角线AC，BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点，求证：四边形EFGH是平行四边形.

查看试题解析
19. 甲、乙两车从A城出发前往B城，在整个行程中，汽车离开A城的距离y与时刻t的对应关系如右图所示.

(1)、A、B两城相距多远？

(2)、哪辆车先出发？哪辆车先到B城？

(3)、甲、乙两车的平均速度分别为多少？

(4)、你还能从图中得到哪些信息？

查看试题解析

20. 射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为（单位：环）：

甲：8，8，7，8，9

乙：5，9，7，10，9

教练根据他们的成绩绘制了如下尚不完整的统计图表：

选手	平均数	众数	中位数	方差
甲	8	b	8	0.4
乙	α	9	c	3.2

根据以上信息，请解答下面的问题：

(1)、α＝， b＝， c＝；

(2)、完成图中表示乙成绩变化情况的折线；

(3)、教练根据这5次成绩，决定选择甲参加射击比赛，教练的理由是什么？

(4)、若选手乙再射击第6次，命中的成绩是8环，则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会.（填“变大”、“变小”或“不变”）

查看试题解析

21. 某商店销售每台A型电脑的利润为100元，销售每台B型电脑的利润为150元，该商店计划一次购进A，B两种型号的电脑共100台，设购进A型电脑x台，这100台电脑的销售总利润为y元.

(1)、求y与x的函数关系式；

(2)、该商店计划一次购进A，B两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，那么商店购进A型、B型电脑各多少台，才能使销售总利润最大？

查看试题解析
22. 如图，正方形ABCD的对角线AC，BD相交于点O，点E是AC的一点，连接EB，过点A做AM⊥BE，垂足为M，AM与BD相交于点F.

(1)、猜想：如图（1）线段OE与线段OF的数量关系为；

(2)、拓展：如图（2），若点E在AC的延长线上，AM⊥BE于点M，AM、DB的延长线相交于点F，其他条件不变，（1）的结论还成立吗？如果成立，请仅就图（2）给出证明；如果不成立，请说明理由.

查看试题解析
23. 如图，在平面直角坐标系中，直线y＝x+2与x轴，y轴分别交于A，B两点，点C（2，m）为直线y＝x+2上一点，直线y＝﹣ $\frac{1}{2}$ x+b过点C．

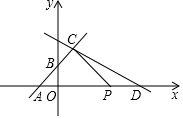(1)、求m和b的值；

(2)、直线y＝﹣ $\frac{1}{2}$ x+b与x轴交于点D，动点P从点D开始以每秒1个单位的速度向x轴负方向运动．设点P的运动时间为t秒．
①若点P在线段DA上，且△ACP的面积为10，求t的值；

②是否存在t的值，使△ACP为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．

查看试题解析