山东省潍坊市高密市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 已知 是正比例函数,则m的值是( )A、8 B、4 C、±3 D、32. 下列属于最简二次根式的是( )A、 B、 C、 D、3. 若式子 有意义,则一次函数 的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 4. 一元一次不等式组 的解集为x>a,且a≠b,则a与b的关系是( )A、a>b B、a<b C、a>b>0 D、a<b<05. 如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( )
4. 一元一次不等式组 的解集为x>a,且a≠b,则a与b的关系是( )A、a>b B、a<b C、a>b>0 D、a<b<05. 如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( ) A、 B、 C、 D、6. 若最简二次根式2 与 是同类二次根式,则a的值为( )A、 B、2 C、﹣3 D、7. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( )
A、 B、 C、 D、6. 若最简二次根式2 与 是同类二次根式,则a的值为( )A、 B、2 C、﹣3 D、7. 均匀的向一个容器内注水,在注水过程中,水面高度 与时间 的函数关系如图所示,则该容器是下列中的( ) A、
A、 B、
B、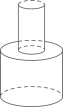 C、
C、 D、
D、 8. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )
8. 下列四组图形中,左边的图形与右边的图形成中心对称的有( )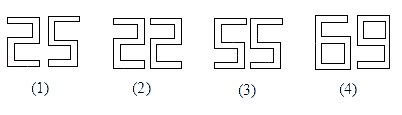 A、1组 B、2组 C、3组 D、4组9. 如图,下列条件中,不能判定△ACD∽△ABC的是( )
A、1组 B、2组 C、3组 D、4组9. 如图,下列条件中,不能判定△ACD∽△ABC的是( )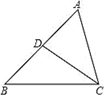 A、∠ADC=∠ACB B、∠B=∠ACD C、∠ACD=∠BCD D、10. 如图所示的四边形,与选项中的四边形一定相似的是( )
A、∠ADC=∠ACB B、∠B=∠ACD C、∠ACD=∠BCD D、10. 如图所示的四边形,与选项中的四边形一定相似的是( ) A、
A、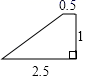 B、
B、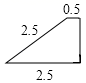 C、
C、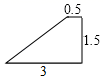 D、
D、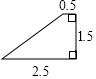 11. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )
11. 如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形AECF的面积为20,DE=2,则AE的长为( )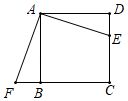 A、4 B、 C、6 D、12. 如图,已知△ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD= AO,OE= BO,OF= CO,得△DEF,有下列说法:
A、4 B、 C、6 D、12. 如图,已知△ABC,任取一点O,连AO,BO,CO,分别取点D,E,F,使OD= AO,OE= BO,OF= CO,得△DEF,有下列说法:①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△DEF与△ABC的周长比为1:3;④△DEF与△ABC的面积比为1:6.
则正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 化简: = .14. 若2x﹣5没有平方根,则x的取值范围为 .15. 请写出一个比2小的无理数是 .16. 如图,平移折线AEB,得到折线CFD,则平移过程中扫过的面积是 .
 17. 若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于 .18. 如图,已知△ABC∽△ADB,若AD=2,CD=2,则AB的长为 .
17. 若三点(1,4),(2,7),(a,10)在同一直线上,则a的值等于 .18. 如图,已知△ABC∽△ADB,若AD=2,CD=2,则AB的长为 . 19. 如图,已知一次函数 的图象为直线,则关于 的方程 的解 .
19. 如图,已知一次函数 的图象为直线,则关于 的方程 的解 .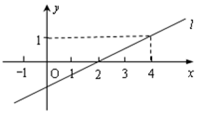 20. 如图,等边△AOB中,点B在x轴正半轴上,点A坐标为(1, ),将△AOB绕点O顺时针旋转15°,此时点A对应点A′的坐标是 .
20. 如图,等边△AOB中,点B在x轴正半轴上,点A坐标为(1, ),将△AOB绕点O顺时针旋转15°,此时点A对应点A′的坐标是 .
三、解答题
-
21. 请从不等式﹣4x>2, , 中任选两个组成一个一元一次不等式组.解出这个不等式组,并在数轴上表示出它的解集.
 22. 二次根式计算:(1)、 ;(2)、 ;(3)、( )÷ ;(4)、 .23. 如图,在 中, ,将 沿 方向向右平移得到 ,若 .
22. 二次根式计算:(1)、 ;(2)、 ;(3)、( )÷ ;(4)、 .23. 如图,在 中, ,将 沿 方向向右平移得到 ,若 . (1)、判断四边形 的形状,并说明理由;(2)、求四边形 的面积.24. 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
(1)、判断四边形 的形状,并说明理由;(2)、求四边形 的面积.24. 如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号) 25. 某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)、求y与x之间的函数表达式;(2)、若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.26. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
25. 某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).(1)、求y与x之间的函数表达式;(2)、若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.26. 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1. (1)、求k、b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集.(3)、若点D在y轴上,且满足S△BCD=2S△BOC , 求点D的坐标.
(1)、求k、b的值;(2)、请直接写出不等式kx+b﹣3x>0的解集.(3)、若点D在y轴上,且满足S△BCD=2S△BOC , 求点D的坐标.