山东省泰安市岱岳区(五四制)2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 已知 ,则 等于( )A、 B、 C、2 D、32. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、3. 已知三个数为3,4,12,若再添加一个数,使这四个数能组成一个比例,那么这个数可以是( )A、1 B、2 C、3 D、44. 下列式子运算正确的是( )A、 B、 C、 D、5. 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2,则矩形的面积为( )
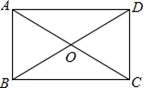 A、2 B、4 C、 D、36. 如图,下列条件中,不能判定△ACD∽△ABC的是( )
A、2 B、4 C、 D、36. 如图,下列条件中,不能判定△ACD∽△ABC的是( )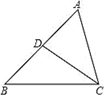 A、∠ADC=∠ACB B、∠B=∠ACD C、∠ACD=∠BCD D、7. 在数轴上用点B表示实数b . 若关于x的一元二次方程x2+bx+1=0有两个相等的实数根,则( )A、 B、 C、 D、8. 点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
A、∠ADC=∠ACB B、∠B=∠ACD C、∠ACD=∠BCD D、7. 在数轴上用点B表示实数b . 若关于x的一元二次方程x2+bx+1=0有两个相等的实数根,则( )A、 B、 C、 D、8. 点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( ) A、点E B、点F C、点H D、点G9. 若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )A、 B、2020 C、2019 D、201810. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标( )
A、点E B、点F C、点H D、点G9. 若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )A、 B、2020 C、2019 D、201810. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(3,0),(﹣2,0),点D在y轴上,则点C的坐标( )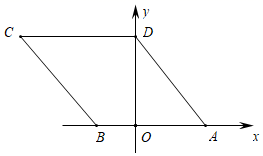 A、(﹣3,4) B、(﹣2,3) C、(﹣5,4) D、(5,4)11. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=10012. 如图, , ,点 在边 上(与 、 不重合),四边形 为正方形,过点 作 ,交 的延长线于点 ,连接 ,交 于点 ,对于下列结论:① ;②四边形 是矩形;③ .其中正确的是( )
A、(﹣3,4) B、(﹣2,3) C、(﹣5,4) D、(5,4)11. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=10012. 如图, , ,点 在边 上(与 、 不重合),四边形 为正方形,过点 作 ,交 的延长线于点 ,连接 ,交 于点 ,对于下列结论:① ;②四边形 是矩形;③ .其中正确的是( )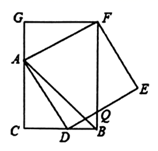 A、①②③ B、①② C、①③ D、②③
A、①②③ B、①② C、①③ D、②③二、填空题
-
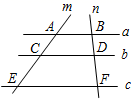
13. 如图,已知直线 ,直线m、n与a、b、c分别交于点A、C、E和B、D、F,如果 , , ,那么 .
 14. 若 是关于 的方程 的一个根,则方程的另一个根是.15. 如图,在菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC= .
14. 若 是关于 的方程 的一个根,则方程的另一个根是.15. 如图,在菱形ABCD中,∠BAD=120°,CF⊥AD于点E,且BC=CF,连接BF交对角线AC于点M,则∠FMC= . 16. 计算: 的结果是.17. 如图,将 沿 所在的直线平移得到 ,如果 , , ,那么 .
16. 计算: 的结果是.17. 如图,将 沿 所在的直线平移得到 ,如果 , , ,那么 .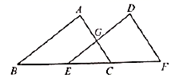 18. 如图, 中,点 是边 上一点, 交 于点 ,若 , , 的面积是1,则 的面积为.
18. 如图, 中,点 是边 上一点, 交 于点 ,若 , , 的面积是1,则 的面积为.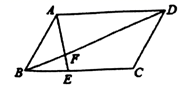
三、解答题
-
19. 用适当的方法解方程.(1)、(2)、20. 在一个边长为(2 +3 )cm的正方形的内部挖去一个长为(2 + )cm,宽为( ﹣ )cm的矩形,求剩余部分图形的面积.21. 如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
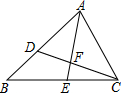 (1)、求证:△ACD∽△ABC;(2)、求 的值.22. 如图所示,有一长方形的空地,长为 米,宽为 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
(1)、求证:△ACD∽△ABC;(2)、求 的值.22. 如图所示,有一长方形的空地,长为 米,宽为 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.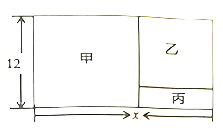 (1)、请用含 的代数式表示正方形乙的边长;(2)、若丙地的面积为 平方米,请求出 的值.23. 如图,在四边形
(1)、请用含 的代数式表示正方形乙的边长;(2)、若丙地的面积为 平方米,请求出 的值.23. 如图,在四边形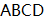 中,
中, 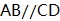 ,
, 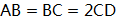 ,E为对角线
,E为对角线 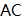 的中点,F为边
的中点,F为边 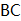 的中点,连接
的中点,连接 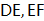 .
. 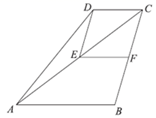 (1)、求证:四边形 为菱形;(2)、连接 交 于点G,若 , ,求 的长.24. 我市晶泰星公司安排 名工人生产甲、乙两种产品,每人每天生产 件甲产品或 件乙产品.根据市场行情测得,甲产品每件可获利 元,乙产品每件可获利 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产 件乙产品,当天每件乙产品平均荻利减少 元,设每天安排 人生产乙产品.(1)、根据信息填表:
(1)、求证:四边形 为菱形;(2)、连接 交 于点G,若 , ,求 的长.24. 我市晶泰星公司安排 名工人生产甲、乙两种产品,每人每天生产 件甲产品或 件乙产品.根据市场行情测得,甲产品每件可获利 元,乙产品每件可获利 元.而实际生产中,生产乙产品需要数外支出一定的费用,经过核算,每生产 件乙产品,当天每件乙产品平均荻利减少 元,设每天安排 人生产乙产品.(1)、根据信息填表:产品种类
每天工人数(人)
每天产量(件)
每件产品可获利润(元)
甲
乙
(2)、若每天生产甲产品可获得的利润比生产乙产品可获得的利润多 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?25. 如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB•EC.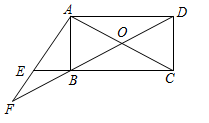 (1)、求证:四边形ABCD是矩形;(2)、延长DB、AE交于点F,若AF=AC,求证:AE=BF.
(1)、求证:四边形ABCD是矩形;(2)、延长DB、AE交于点F,若AF=AC,求证:AE=BF.