云南省曲靖市罗平县2020年数学中考一模试卷
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 下列各数是有理数的是( )A、 B、 C、 D、π2. 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
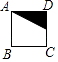 A、
A、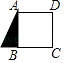 B、
B、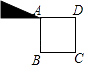 C、
C、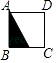 D、
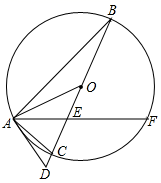
D、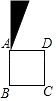 3. 新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )A、8×10﹣8 B、8×10﹣7 C、80×10﹣9 D、0.8×10﹣74. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(-2ab3)2=-4a2b6 C、3a2-2a3=a6 D、a3-a=a(a+1)(a-1)5. 式子 有意义,则实数a的取值范围是( )A、a≥-1 B、a≠2 C、a≥-1且a≠2 D、a>26. 一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )A、30° B、45° C、60° D、80°7. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
3. 新冠病毒的直径最小大约为0.00000008米,这个数用科学记数法表示为( )A、8×10﹣8 B、8×10﹣7 C、80×10﹣9 D、0.8×10﹣74. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(-2ab3)2=-4a2b6 C、3a2-2a3=a6 D、a3-a=a(a+1)(a-1)5. 式子 有意义,则实数a的取值范围是( )A、a≥-1 B、a≠2 C、a≥-1且a≠2 D、a>26. 一个正多边形的内角和为1080°,则这个正多边形的每个外角为( )A、30° B、45° C、60° D、80°7. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )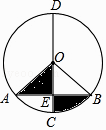 A、4π﹣4 B、2π﹣4 C、4π D、2π8. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹。
A、4π﹣4 B、2π﹣4 C、4π D、2π8. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹。步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
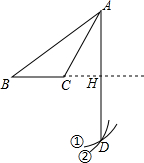 A、BH垂直平分线段AD B、AC平分∠BAD C、S△ABC=BC⋅AH D、AB=AD
A、BH垂直平分线段AD B、AC平分∠BAD C、S△ABC=BC⋅AH D、AB=AD二、填空题
-
9. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是;今有两数若其意义相反,则分别叫做正数与负数.若气温为零上 记作 ,则 表示气温为.10. 因式分解: .11. 如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB=°.
 12. 小明沿着坡度i为1∶ 的直路向上走了50 m,则小明沿垂直方向升高了m.
12. 小明沿着坡度i为1∶ 的直路向上走了50 m,则小明沿垂直方向升高了m.
13. 关于 的一元二次方程 无实数根,则 的取值范围为.14. 如图,过点 作直线 的垂线,垂足为点 ,过点 作 轴,垂足为点 ,过点 作 ,垂足为点 …,这样依次下去,得到一组线段 …,则线段 的长为.
三、解答题
-
15. 计算:(-1)2-|-7|+
 ×(2017-π)0+(
×(2017-π)0+(  )-2 16. 先化简,再求值: ),其中 .17. 如图,点 , , , 在同一直线上, AD=EB , , .求证: .
)-2 16. 先化简,再求值: ),其中 .17. 如图,点 , , , 在同一直线上, AD=EB , , .求证: . 18. 某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.(1)、求这种笔和本子的单价;(2)、该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.19. 为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生的期末数学成绩为样本,分为 ( 分)、 ( 分)、 ( 分)、 ( 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
18. 某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.(1)、求这种笔和本子的单价;(2)、该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.19. 为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生的期末数学成绩为样本,分为 ( 分)、 ( 分)、 ( 分)、 ( 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题: (1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图.(3)、这个学校九年级共有学生 人,若分数为 分(含 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生大约有多少?20. 甲、乙两人进行摸牌游戏,现有三张形状大小完全相同的牌,正面分别标有数字 , , ,将三张牌背面朝上,洗匀后放在桌子上.(1)、甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;(2)、若两人抽取的数字和为 的倍数,则甲获胜;若抽取的数字和为 的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.21. 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y= .
(1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图.(3)、这个学校九年级共有学生 人,若分数为 分(含 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生大约有多少?20. 甲、乙两人进行摸牌游戏,现有三张形状大小完全相同的牌,正面分别标有数字 , , ,将三张牌背面朝上,洗匀后放在桌子上.(1)、甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;(2)、若两人抽取的数字和为 的倍数,则甲获胜;若抽取的数字和为 的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.21. 宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:y= .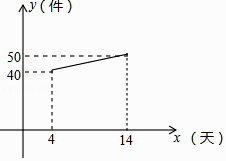 (1)、工人甲第几天生产的产品数量为70件?(2)、设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
(1)、工人甲第几天生产的产品数量为70件?(2)、设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?