贵州省安顺市2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2017-09-21 类型:期末考试
一、单项选择题.
-
1. 下列计算正确的是( )A、=±3 B、|﹣3|=﹣3 C、=3 D、﹣32=92. 下列调查适合抽样调查的是( )A、审核书稿中的错别字 B、对某社区的卫生死角进行调查 C、对八名同学的身高情况进行调查 D、对中学生目前的睡眠情况进行调查3. 实数 , ,0,﹣π, , ,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
A、1 B、2 C、3 D、44. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 5. 如图,下列条件中不能判定AB∥CD的是( )
5. 如图,下列条件中不能判定AB∥CD的是( )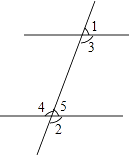 A、∠3=∠4 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠56. 下列语句:
A、∠3=∠4 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠56. 下列语句:①相等的角是对顶角;
②如果两条直线被第三条直线所截,那么同位角相等;
③过直线外一点有且只有一条直线与已知直线平行;
④平行线间的距离处处相等.
其中正确的命题是( )
A、①② B、②③ C、③④ D、①④7. 方程组 的解为 ,则a、b的值分别为( )A、1,2 B、5,1 C、2,1 D、2,38. 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
A、 B、 C、 D、9. 如果P(a+b,ab)在第二象限,那么点Q(a,﹣b)在第( )象限.A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=20°,则∠EPF=( ) A、70° B、65° C、55° D、45°
A、70° B、65° C、55° D、45°二、填空题
-
11. 在平面直角坐标系中,点P(m,m﹣3)在第四象限内,则m的取值范围是 .12. 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD,若∠ECA的度数为40°,则∠GFB的度数为 .
 13. 4xa+2b﹣5﹣2y3a﹣b﹣3=8是二元一次方程,那么4a+b= .14.
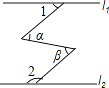
13. 4xa+2b﹣5﹣2y3a﹣b﹣3=8是二元一次方程,那么4a+b= .14.如图,直线l1∥l2 , ∠α=∠β,∠1=50°,则∠2= .
 15.
15.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是 cm,点A到BC的距离是 cm,C到AB的距离是 cm.
 16. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根为17. 若关于x、y方程组 的解为x、y,且﹣2<k<4,则x﹣y的取值范围是 .
16. 已知 是二元一次方程组 的解,则2m﹣n的算术平方根为17. 若关于x、y方程组 的解为x、y,且﹣2<k<4,则x﹣y的取值范围是 .三、解答题
-
18. 解方程组: .19. 解不等式组 ,并把解集在数轴上表示出来.
 20.
20.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
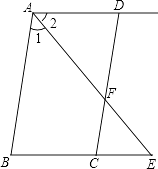
∵AB∥DC(已知)
∴∠1=∠CFE()
∵AE平分∠BAD(已知)
∴∠1=∠2 (角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=(等量代换)
∴AD∥BC ()
21. 如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1 , 点P的对应点为P1(a+6,b﹣2). (1)、直接写出点C1的坐标;(2)、在图中画出△A1B1C1;(3)、求△AOA1的面积.22. 某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
(1)、直接写出点C1的坐标;(2)、在图中画出△A1B1C1;(3)、求△AOA1的面积.22. 某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题. (1)、将条形统计图补充完整;(2)、本次抽样调查的样本容量是;(3)、已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.23. “全名阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1600元,20本文学名著比20本动漫书多400元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).(1)、求每本文学名著和动漫书各多少元?(2)、若学校要求购买动漫书比文学名著多20本,而且文学名著不低于25本,总费用不超过2000,请求出所有符合条件的购书方案.
(1)、将条形统计图补充完整;(2)、本次抽样调查的样本容量是;(3)、已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.23. “全名阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1600元,20本文学名著比20本动漫书多400元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).(1)、求每本文学名著和动漫书各多少元?(2)、若学校要求购买动漫书比文学名著多20本,而且文学名著不低于25本,总费用不超过2000,请求出所有符合条件的购书方案.