山东省乐陵市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 如果下列各组数是三角形的三边长,那么能组成直角三角形的一组数是( )A、 , , B、 , , C、 , , D、 , ,2. 下列函数:① ;② ;③ ;④ ;⑤ .其中,是一次函数的有( )A、1个 B、2个 C、3个 D、4个3. 在 中, ,则 的度数为( )A、 B、 C、 D、4. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
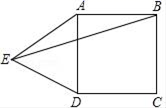 A、45° B、15° C、10° D、125°5. 直线 与 轴、 轴的交点坐标分别是( )A、 , B、 , C、 , D、 ,6. 关于一组数据:1,5,6,3,5,下列说法错误的是( )A、平均数是4 B、众数是5 C、中位数是6 D、方差是3.27. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
A、45° B、15° C、10° D、125°5. 直线 与 轴、 轴的交点坐标分别是( )A、 , B、 , C、 , D、 ,6. 关于一组数据:1,5,6,3,5,下列说法错误的是( )A、平均数是4 B、众数是5 C、中位数是6 D、方差是3.27. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表数据,从中选择一名成绩好且发挥稳定的参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁8. 若关于x的方程 是一元二次方程,则m的取值范围是( )A、 . B、 . C、 D、 .9. 下列说法错误的是( )A、必然事件发生的概率为 B、不可能事件发生的概率为 C、有机事件发生的概率大于等于 、小于等于 D、概率很小的事件不可能发生10. 某商品的价格为100元,连续两次降x%后的价格是81元,则 为( )A、9 B、10 C、19 D、811. 为了增强学生体质,学校发起评选“健步达人”活动,小明用计步器记录自己一个月(30天)每天走的步数,并绘制成如下统计表:步数(万步)
1.0
1.2
1.1
1.4
1.3
天数
3
3
5
7
12
在每天所走的步数这组数据中,众数和中位数分别是( )
A、1.3,1.1 B、1.3,1.3 C、1.4,1.4 D、1.3,1.412. 公式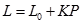 表示当重力为P时的物体作用在弹簧上时弹簧的长度.
表示当重力为P时的物体作用在弹簧上时弹簧的长度. 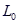 表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P13. 如图,在 中, , , ,则点 到 的距离为( )
表示弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( ) A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P13. 如图,在 中, , , ,则点 到 的距离为( ) A、 B、 C、 D、14. 一个口袋中装有3个绿球,2个黄球,每个球除颜色外其它都相同,搅均后随机地从中摸出两个球都是绿球的概率是( )A、 B、 C、 D、15. 如图是甲、乙两个探测气球所在位置的海拔高度y(单位:m)关于上升时间x(单位: )的函数图象.有下列结论:
A、 B、 C、 D、14. 一个口袋中装有3个绿球,2个黄球,每个球除颜色外其它都相同,搅均后随机地从中摸出两个球都是绿球的概率是( )A、 B、 C、 D、15. 如图是甲、乙两个探测气球所在位置的海拔高度y(单位:m)关于上升时间x(单位: )的函数图象.有下列结论:①当 时,两个探测气球位于同一高度
②当 时,乙气球位置高;
③当 时,甲气球位置高;
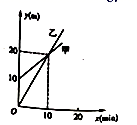
其中,符合题意结论的个数是( )
A、 个 B、 个 C、 个 D、 个16. 若关于x的方程kx2﹣3x﹣ =0有实数根,则实数k的取值范围是( )A、k=0 B、k≥﹣1 C、k≥﹣1且k≠0 D、k>﹣1二、填空题
-
17. 工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这依据的道理是: .
 18. 方程 的解为 .19. 若 , 是一元二次方程 的两个实数根,则 .20. 小玲在一次班会中参加知识抢答活动,现有语文题 道,数学题 道,综合题 道,她从中随机抽取 道,抽中数学题的概率是 .21. 在一次智力抢答比赛中,四个小组回答正确的情况如下图.这四个小组平均符合题意回答道题目?(结果取整数)
18. 方程 的解为 .19. 若 , 是一元二次方程 的两个实数根,则 .20. 小玲在一次班会中参加知识抢答活动,现有语文题 道,数学题 道,综合题 道,她从中随机抽取 道,抽中数学题的概率是 .21. 在一次智力抢答比赛中,四个小组回答正确的情况如下图.这四个小组平均符合题意回答道题目?(结果取整数) 22. 已知一次函数 的图象如图,根据图中息请写出不等式 的解集为 .
22. 已知一次函数 的图象如图,根据图中息请写出不等式 的解集为 .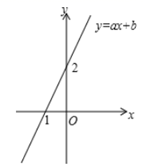 23.
23.如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3 , 则原铁皮的宽为 cm.
 24. 如图,在矩形纸片 中, , 折叠纸片,使点 落在 边上的点 处,折痕为 ,当点 在 边上移动时,折痕的端点 , 也随之移动,若限定点 , 分别在 , 边上移动,则点 在 边上可移动的最大距离为 .
24. 如图,在矩形纸片 中, , 折叠纸片,使点 落在 边上的点 处,折痕为 ,当点 在 边上移动时,折痕的端点 , 也随之移动,若限定点 , 分别在 , 边上移动,则点 在 边上可移动的最大距离为 .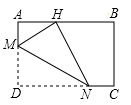
三、解答题
-
25. 解方程:(1)、(2)、26. 春季流感爆发,有一人患了流感,经过两轮传染后共有 人患了流感,(1)、每轮传染中平均一个人传染了几个人?(2)、经过三轮传染后共有多少人患了流感?27. 如图,四边形 是正方形,点 是 边上的任意一点, 于点 , ,且交 于点 ,求证:
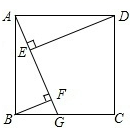 (1)、(2)、28. 随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷每人必选且只选一种,在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、(2)、28. 随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷每人必选且只选一种,在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: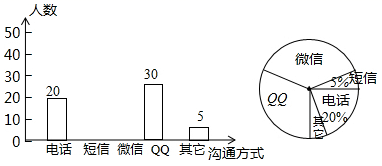 (1)、这次统计共抽查了名学生;在扇形统计图中,表示“ ”的扇形所占百分数为;(2)、将条形统计图补充完整;(3)、该校共有 名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“ ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.29. 如图,四边形 为菱形,已知 , .
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“ ”的扇形所占百分数为;(2)、将条形统计图补充完整;(3)、该校共有 名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“ ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.29. 如图,四边形 为菱形,已知 , .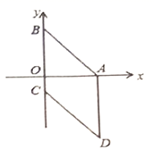 (1)、求点 的坐标;(2)、求经过点 , 两点的一次函数的解析式.(3)、求菱形 的面积.30. 已知关于x的一元二次方程 .(1)、当m为何值时,方程有两个不相等的实数根;(2)、若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.31. 再读教材:
(1)、求点 的坐标;(2)、求经过点 , 两点的一次函数的解析式.(3)、求菱形 的面积.30. 已知关于x的一元二次方程 .(1)、当m为何值时,方程有两个不相等的实数根;(2)、若边长为5的菱形的两条对角线的长分别为方程两根的2倍,求m的值.31. 再读教材:宽与长的比是 (约为0.618)的矩形叫做黄金矩形,黄金矩形给我们以协调,匀称的美感.世界各国许多著名的建筑.为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为2的矩形纸片折叠黄金矩形.(提示; MN=2)
第一步,在矩形纸片一端.利用图①的方法折出一个正方形,然后把纸片展平.
第二步,如图②.把这个正方形折成两个相等的矩形,再把纸片展平.

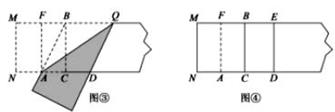
第三步,折出内侧矩形的对角线 AB,并把 AB折到图③中所示的AD处,
第四步,展平纸片,按照所得的点D折出DE,使DE⊥ND,则图④中就会出现黄金矩形,
问题解决:
(1)、图③中AB=(保留根号);(2)、如图③,判断四边形BADQ的形状,并说明理由;(3)、请写出图④中所有的黄金矩形,并选择其中一个说明理由.(4)、结合图④.请在矩形BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.32. 如图1,在平面直角坐标系中,一次函数 的图象与 轴, 轴分别交于点 ,点 ,过点 作 轴,垂足为点 ,过点 作 轴,垂足为点 ,两条垂线相交于点 .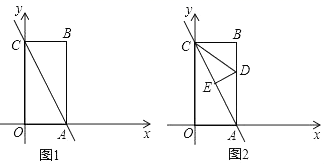 (1)、线段 , , 的长分别为 , , ;(2)、折叠图1中的 ,使点 与点 重合,再将折叠后的图形展开,折痕 交 于点 ,交 于点 ,连接 ,如图2.
(1)、线段 , , 的长分别为 , , ;(2)、折叠图1中的 ,使点 与点 重合,再将折叠后的图形展开,折痕 交 于点 ,交 于点 ,连接 ,如图2.①求线段 的长;
②在 轴上,是否存在点 ,使得 为等腰三角形?若存在,请直接写出符合条件的所有点 的坐标;若不存在,请说明理由.