山东省济宁市任城区2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 三角形在正方形网格纸中的位置如图所示,则 的值是( )
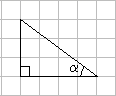 A、 B、 C、 D、2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根4. 某药品经过两次降价,每瓶零售价由168元降为128元。已知两次降价的百分率相同,每次降价的百分率为x ,根据题意列方程得( )A、 B、 C、 D、5. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、6. 已知关于 的方程 的两根互为倒数,则 的值为( )A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A、 B、 C、 D、2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根4. 某药品经过两次降价,每瓶零售价由168元降为128元。已知两次降价的百分率相同,每次降价的百分率为x ,根据题意列方程得( )A、 B、 C、 D、5. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、6. 已知关于 的方程 的两根互为倒数,则 的值为( )A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( ) A、3:4 B、9:16 C、9:1 D、3:18. 如图, 中, 是斜边 上的高, ,那么 等于( )
A、3:4 B、9:16 C、9:1 D、3:18. 如图, 中, 是斜边 上的高, ,那么 等于( )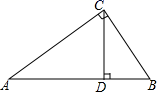 A、 B、 C、 D、9. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A、 B、 C、 D、9. 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )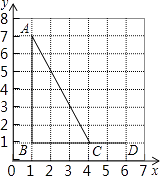 A、(6,0) B、(6,3) C、(6,5) D、(4,2)10. 下表是小红填写的实践活动报告的部分内容:
A、(6,0) B、(6,3) C、(6,5) D、(4,2)10. 下表是小红填写的实践活动报告的部分内容: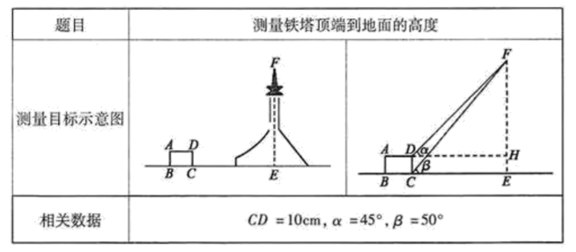
设铁塔顶端到地面的高度 为 ,根据以上条件,可以列出的方程为( )
A、 B、 C、 D、二、填空题
-
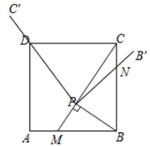
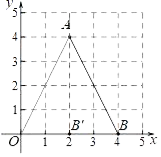
11. 若2m= 3n,那么m︰n=.12. 如图,在平面直角坐标系xOy中,有两点A(2,4),B(4,0),以原点O为位似中心,把△OAB缩小得到△OA'B'.若B'的坐标为(2,0),则点A'的坐标为.
 13. 《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有句五步,股十二步.问句中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为 .
13. 《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有句五步,股十二步.问句中容方几何.”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为 .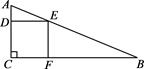 14. 图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机侧立面夹角 .当双翼收起时,可以通过闸机的物体的最大宽度 为
14. 图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点 与 之间的距离为 ,双翼的边缘 ,且与闸机侧立面夹角 .当双翼收起时,可以通过闸机的物体的最大宽度 为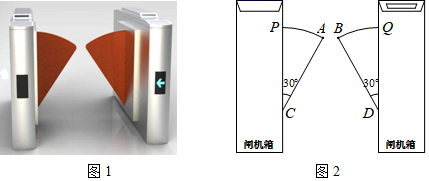 15. 某校要设计一座 高的雕像(如图),使雕像的点 (肚脐)为线段 (全身)的黄金分割点,上部 (肚脐以上)与下部 (肚脐以下)的高度比为黄金比.则雕像下部设计的高度应该为(结果精确到 )米.( ,结果精确到 ).
15. 某校要设计一座 高的雕像(如图),使雕像的点 (肚脐)为线段 (全身)的黄金分割点,上部 (肚脐以上)与下部 (肚脐以下)的高度比为黄金比.则雕像下部设计的高度应该为(结果精确到 )米.( ,结果精确到 ).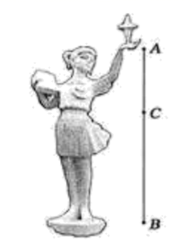
三、解答题
-
16. 计算: .17. 关于x的方程x2+(2k+1)x+k2﹣1=0有两个不相等的实数根.(1)、求实数k的取值范围;(2)、若k为负整数,求此时方程的根.18. 下图是某大桥的斜拉索部分效果图,为了测得斜拉索顶端 距离海平面的高度,先测出斜拉索底端 到桥塔的距离( 的长)约为 米,又在 点测得 点的仰角为 ,测得 点的俯角为 ,求斜拉索顶端 点到海平面 点的距离( 的长). ( )
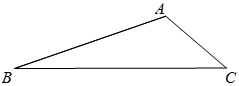
 19. 如图,在 中, 分别是边 上的点,连接 ,且 .
19. 如图,在 中, 分别是边 上的点,连接 ,且 .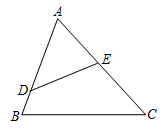 (1)、求证: ;(2)、如果 是 的中点, ,求 的长,20. 已知在 中, 是边 上的一点, 的角平分线交 于点 ,且 ,求证: .
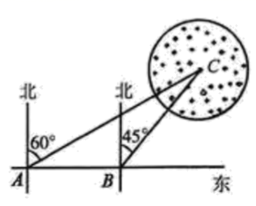
(1)、求证: ;(2)、如果 是 的中点, ,求 的长,20. 已知在 中, 是边 上的一点, 的角平分线交 于点 ,且 ,求证: .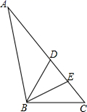 21. 今年人夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在 处测得航标 在北偏东 方向上,前进 米到达 处,又测得航标 在北偏东 方向上,如图在以航标 为圆心, 米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险? ( )
21. 今年人夏以来,松花江哈尔滨段水位不断下降,达到历史最低水位,一条船在松花江某水段自西向东沿直线航行,在 处测得航标 在北偏东 方向上,前进 米到达 处,又测得航标 在北偏东 方向上,如图在以航标 为圆心, 米长为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险? ( )