山东省济南市历下区2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2020-06-23 类型:期末考试
一、单选题
-
1. 道路千万条,安全第一条,下列交通标志是中心对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 把代数式2x2﹣18分解因式,结果正确的是( )A、2(x2﹣9) B、2(x﹣3)2 C、2(x+3)(x﹣3) D、2(x+9)(x﹣9)3. 一元二次方程 配方后可化为( )A、 B、 C、 D、4. 化简 的结果为( )A、﹣ B、﹣y C、 D、5. 关于x的分式方程 有增根,则a的值为( )A、﹣3 B、﹣5 C、0 D、26. 如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )
2. 把代数式2x2﹣18分解因式,结果正确的是( )A、2(x2﹣9) B、2(x﹣3)2 C、2(x+3)(x﹣3) D、2(x+9)(x﹣9)3. 一元二次方程 配方后可化为( )A、 B、 C、 D、4. 化简 的结果为( )A、﹣ B、﹣y C、 D、5. 关于x的分式方程 有增根,则a的值为( )A、﹣3 B、﹣5 C、0 D、26. 如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )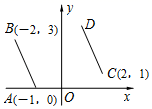 A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)7. 如图,A,B两地被池塘隔开,小康通过下列方法测出了A,B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A,B间的距离.下列有关他这次探究活动的结论中,错误的是( )
A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)7. 如图,A,B两地被池塘隔开,小康通过下列方法测出了A,B间的距离:先在AB外选一他点C,然后测出AC,BC的中点M、N,并测量出MN的长为18m,由此他就知道了A,B间的距离.下列有关他这次探究活动的结论中,错误的是( ) A、AB=36m B、MN∥AB C、MN= CB D、CM= AC8. 某地开挖一条480米的渠道,开工后,实际每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么所列方程正确的是( )A、 B、 C、 D、9. 如图,将 绕点 顺时针旋转 得到 .若点 在同一条直线上,则 的度数是( )
A、AB=36m B、MN∥AB C、MN= CB D、CM= AC8. 某地开挖一条480米的渠道,开工后,实际每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么所列方程正确的是( )A、 B、 C、 D、9. 如图,将 绕点 顺时针旋转 得到 .若点 在同一条直线上,则 的度数是( ) A、 B、 C、 D、10. 如图, 的对角线 , 交于点 , , , ,那么 的长为( )
A、 B、 C、 D、10. 如图, 的对角线 , 交于点 , , , ,那么 的长为( ) A、 B、 C、3 D、411. 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点 分别作 和 的垂线,垂足为C,D.当矩形 的面积为1时,点 的坐标为( )
A、 B、 C、3 D、411. 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点 分别作 和 的垂线,垂足为C,D.当矩形 的面积为1时,点 的坐标为( ) A、 B、 C、 或 D、 或12. 如图,在平行四边形 中,对角线 、 相交于 , , 、 、 分别是 、 、 的中点,下列结论:
A、 B、 C、 或 D、 或12. 如图,在平行四边形 中,对角线 、 相交于 , , 、 、 分别是 、 、 的中点,下列结论:① ;② ;③ ;④ 平分 ;⑤四边形 是菱形.
其中正确的是( )
 A、①②③ B、①③④ C、①②⑤ D、②③⑤
A、①②③ B、①③④ C、①②⑤ D、②③⑤二、填空题
-
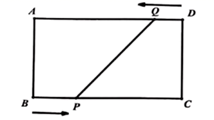
13. 分解因式:x2-2x+1=.14. 若分式 的值为0,则x的值为 .15. 若n边形的内角和是它的外角和的2倍,则n=.16. 已知关于 的方程 的一个解为1,则它的另一个解是 .17. 如图,在矩形 中, ,点 和点 分别从点 和点 同时出发,按逆时针方向沿矩形 的边运动,点 和点 的速度分别为 和 ,当四边形 初次为矩形时,点 和点 运动的时间为 .
 18. 如图, 为等边三角形, , ,点 为线段 上的动点,连接 ,以 为边作等边 ,连接 ,则线段 的最小值为 .
18. 如图, 为等边三角形, , ,点 为线段 上的动点,连接 ,以 为边作等边 ,连接 ,则线段 的最小值为 .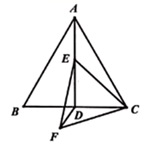 19. 设 是满足不等式 的正整数,且关于 的二次方程 的两根都是正整数,则正整数 的个数为 .20. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线l于点 ,以 为边作正方形 ;……按此规律操作下去,得到的正方形 的面积是 .
19. 设 是满足不等式 的正整数,且关于 的二次方程 的两根都是正整数,则正整数 的个数为 .20. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线l于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线l于点 ,以 为边作正方形 ;……按此规律操作下去,得到的正方形 的面积是 .
三、解答题
-
21. 解下列方程(1)、 ;(2)、 ;(3)、 .22. 如图,在▱ABCD中,点E,F在对角线AC上,且AE=CF.求证:
 (1)、DE=BF;(2)、四边形DEBF是平行四边形.23. 阅读下列材料:
(1)、DE=BF;(2)、四边形DEBF是平行四边形.23. 阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.
下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.
解:设x2﹣4x=y
原式=(y+1)(y+7)+9(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
请根据上述材料回答下列问题:
(1)、小涵同学的解法中,第二步到第三步运用了因式分解的 ;A、提取公因式法 B、平方差公式法 C、完全平方公式法(2)、老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;(3)、请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.24. 如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F. (1)、求证:△AEF≌△DEB;(2)、求证:四边形ADCF是菱形.25. 如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为 cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒.
(1)、求证:△AEF≌△DEB;(2)、求证:四边形ADCF是菱形.25. 如图是一张长20cm、宽12cm的矩形纸板,将纸板四个角各剪去一个边长为 cm的正方形,然后将四周突出部分折起,可制成一个无盖纸盒. (1)、这个无盖纸盒的长为cm,宽为cm;(用含x的式子表示)(2)、若要制成一个底面积是180m2的无盖长方体纸盒,求 的值.26. 如图①,四边形 和四边形 都是正方形,且 , ,正方形 固定,将正方形 绕点 顺时针旋转 角( ).
(1)、这个无盖纸盒的长为cm,宽为cm;(用含x的式子表示)(2)、若要制成一个底面积是180m2的无盖长方体纸盒,求 的值.26. 如图①,四边形 和四边形 都是正方形,且 , ,正方形 固定,将正方形 绕点 顺时针旋转 角( ). (1)、如图②,连接 、 ,相交于点 ,请判断 和 是否相等?并说明理由;(2)、如图②,连接 ,在旋转过程中,当 为直角三角形时,请直接写出旋转角 的度数;(3)、如图③,点 为边 的中点,连接 、 、 ,在正方形 的旋转过程中, 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.27. 如图①,在平面直角坐标系中,直线 : 分别与 轴、 轴交于点 、 ,且与直线 : 交于点 ,以线段 为边在直线 的下方作正方形 ,此时点 恰好落在 轴上.
(1)、如图②,连接 、 ,相交于点 ,请判断 和 是否相等?并说明理由;(2)、如图②,连接 ,在旋转过程中,当 为直角三角形时,请直接写出旋转角 的度数;(3)、如图③,点 为边 的中点,连接 、 、 ,在正方形 的旋转过程中, 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.27. 如图①,在平面直角坐标系中,直线 : 分别与 轴、 轴交于点 、 ,且与直线 : 交于点 ,以线段 为边在直线 的下方作正方形 ,此时点 恰好落在 轴上. (1)、求出 三点的坐标.(2)、求直线 的函数表达式.(3)、在(2)的条件下,点 是射线 上的一个动点,在平面内是否存在点 ,使得以 、 、 、 为顶点的四边形是菱形?若存在,直接写出点 的坐标;若不存在,请说明理由.
(1)、求出 三点的坐标.(2)、求直线 的函数表达式.(3)、在(2)的条件下,点 是射线 上的一个动点,在平面内是否存在点 ,使得以 、 、 、 为顶点的四边形是菱形?若存在,直接写出点 的坐标;若不存在,请说明理由.