辽宁省沈阳市2020年数学中考模拟试卷(4月)
试卷更新日期:2020-06-23 类型:中考模拟
一、选择题
-
1. 下列实数中,最小的是( )A、0 B、﹣7 C、﹣2 D、42. 据报道,2020年某市户籍人口中,60岁以上的老人有1230000人,预计未来五年该市人口“老龄化”还将提速.将1230000用科学记数法表示为( )A、12.3×105 B、1.23×105 C、0.12×106 D、1.23×1063. 如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )
 A、
A、 B、
B、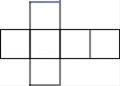 C、
C、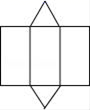 D、
D、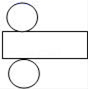 4. 不等式x-1>0的解在数轴上表示为( )A、
4. 不等式x-1>0的解在数轴上表示为( )A、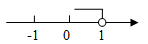 B、
B、 C、
C、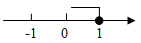 D、
D、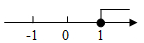 5. 下列等式,错误的是( )A、5y3•3y5=15y8 B、(﹣5a5b3c)÷(15a4b)=﹣ ab2c C、(π﹣3)0=1 D、(﹣xy)3=﹣xy36. 点(﹣2,3)关于y轴的对称点的坐标为( )A、(﹣2,﹣3) B、(2,3) C、(﹣2,3) D、(2,﹣3)7. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )
5. 下列等式,错误的是( )A、5y3•3y5=15y8 B、(﹣5a5b3c)÷(15a4b)=﹣ ab2c C、(π﹣3)0=1 D、(﹣xy)3=﹣xy36. 点(﹣2,3)关于y轴的对称点的坐标为( )A、(﹣2,﹣3) B、(2,3) C、(﹣2,3) D、(2,﹣3)7. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y (k>0,x>0)的图象经过AC的中点D,则k的值为( )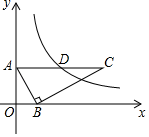 A、4 B、5 C、6 D、88. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A、4 B、5 C、6 D、88. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
A、30° B、40° C、50° D、60°9. 第二届“红色日记”征文大赛于2020年1月12日正式启动,征文内容分为两部分:“不忘初心”和“红色传承”.其中五位评委给参赛者小亮的征文评分分别为:88、92、90、93、88,则这组数据的众数是 ( )A、88 B、90 C、92 D、9310. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.其中,正确结论的个数是( )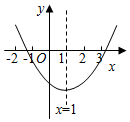 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 因式分解4x2+12xy+9y2=.12. 如图,小正方形边长为1,则△ABC中AC边上的高等于.
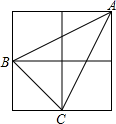 13. 如图,正方形ABCD的边长为4厘米,则图中阴影部分的面积为.
13. 如图,正方形ABCD的边长为4厘米,则图中阴影部分的面积为.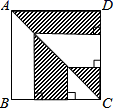 14. 一个口袋中装有2个红球、3个绿球、5个黄球,每个球除颜色外其它都相同,搅均匀后随机从中摸出一个球是绿球的概率是 .15. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于.
14. 一个口袋中装有2个红球、3个绿球、5个黄球,每个球除颜色外其它都相同,搅均匀后随机从中摸出一个球是绿球的概率是 .15. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于.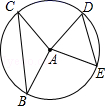 16. 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为.
16. 如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为.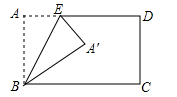
三、解答题
-
17. 计算:18. 四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.(1)、从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为.(2)、从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.19. 2015﹣2016年CBA联赛,吉林九台农商行队把长春体育馆作为自己的主场,小球迷“球球”对自己学校部分学生对去赛场为球队加油助威进行了抽样调查,根据收集到的数据绘制了如下的统计图表.(调查情况说明:A:特别愿意去;B:愿意去;C:去不去都行;D:不愿意去)
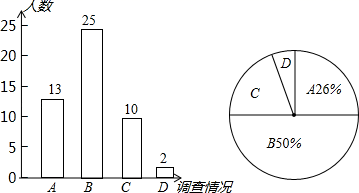 (1)、求出不愿意去的学生的人数占被调查总人数的百分比;(2)、求出扇形统计图中C所在的扇形圆心角的度数;(3)、若该校学生共有2000人,请你估计特别愿意去加油助威的学生共有多少人?20. 如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC.
(1)、求出不愿意去的学生的人数占被调查总人数的百分比;(2)、求出扇形统计图中C所在的扇形圆心角的度数;(3)、若该校学生共有2000人,请你估计特别愿意去加油助威的学生共有多少人?20. 如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC. (1)、求证:△AOE≌△BOF;(2)、求证:四边形BCEF是矩形.21. 为中华人民共和国成立70周年献礼,某灯具厂计划加工6000套彩灯,为尽快完成任务,实际每天加工彩灯的数量是原计划的1.5倍,结果提前5天完成任务.求该灯具厂原计划每天加工这种彩灯的数量.22. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,
(1)、求证:△AOE≌△BOF;(2)、求证:四边形BCEF是矩形.21. 为中华人民共和国成立70周年献礼,某灯具厂计划加工6000套彩灯,为尽快完成任务,实际每天加工彩灯的数量是原计划的1.5倍,结果提前5天完成任务.求该灯具厂原计划每天加工这种彩灯的数量.22. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD, (1)、求证:CD是⊙O的切线;(2)、若BC=6,tan∠CDA= ,求CD的长.23. 如图,直线l:y=﹣ x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动.
(1)、求证:CD是⊙O的切线;(2)、若BC=6,tan∠CDA= ,求CD的长.23. 如图,直线l:y=﹣ x+2与x轴、y轴分别交于A、B两点,动点M从点A以每秒1个单位的速度沿x轴向左移动. (1)、求A、B两点的坐标;(2)、将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;(3)、设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.24. 如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)、求A、B两点的坐标;(2)、将直线l向上平移4个单位后得到直线l',交y轴于点C.求直线l′的函数表达式;(3)、设点M的移动时间为t,当t为何值时,△COM≌△AOB,并求出此时点M的坐标.24. 如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN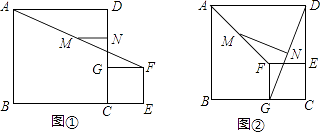 (1)、线段MN和GD的数量关系是 , 位置关系是;(2)、将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;(3)、已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.25. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
(1)、线段MN和GD的数量关系是 , 位置关系是;(2)、将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;(3)、已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.25. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
 (1)、分别求出图中直线和抛物线的函数表达式;(2)、连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(1)、分别求出图中直线和抛物线的函数表达式;(2)、连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.